Android Map数据结构全面总结分析
作者:流浪汉kylin
前言
上一篇讲了Collection、Queue和Deque、List或Set,没看的朋友可以去简单看看,这一篇主要讲和Map相关的数据结构。
Map
上篇有介绍过,Map是另一种数据结构,它独立于Collection,它的是一个接口,它的抽象实现是AbstractMap,它内部是会通过Set来实现迭代器
Set<Map.Entry<K, V>> entrySet();
是和Set有关联的,思想上主要以key-value的形式存储数据,但是具体的实现会交给子类去实现。
ArrayMap
ArrayMap和ArraySet一样,内部用两个数组实现int[] mHashes好Object[] mArray
不同于ArraySet的是,ArraySet的mHashes是用Object的hash,而ArrayMap的mHashes是用key的hash。
TreeMap
上一篇讲的TreeSet内部也是用的TreeMap。TreeMap是一个红黑树的数据结构,如果不了解红黑树的话,直接看会比较懵逼,不过没关系,我们可以往上一级去看,红黑树其实是一种二叉搜索树,那什么是二叉搜索树呢?简单来说,二叉搜索树是任何一个节点的左子树都小于当前节点,任何一个节点的右子树都大于当前节点。
这样讲就更容易能理解了吧。那这棵树的顺序就是中序遍历的顺序,它也符合二分查找的条件。如果还是不理解的话可以先去了解一下二叉搜索树,这比红黑树更容易理解。二叉搜索树在插入节点之后,要实现平衡,通常可以通过左旋和右旋去实现(这个算法这里也不详细说,感兴趣的可以自己去了解,不感兴趣的可以先记住这个概念)。而红黑树要达到平衡,通过左旋和右旋之外还有可能需要实现变色,这个相对于二叉搜索树来说会相对更加复杂。但是没关系,先记住这个概念。它的特点主要是查找通过二分查找,插入会通过左旋右旋和变色来维持平衡。
这里也可以扩展一下红黑树的特征,但是不会详细的介绍
1. 结点是红色或黑色
2. 根结点是黑色
3. 所有叶子都是黑色
4. 每个红色结点的两个子结点都是黑色
5. 从任一结点到其每个叶子的所有路径都包含相同数目的黑色结点
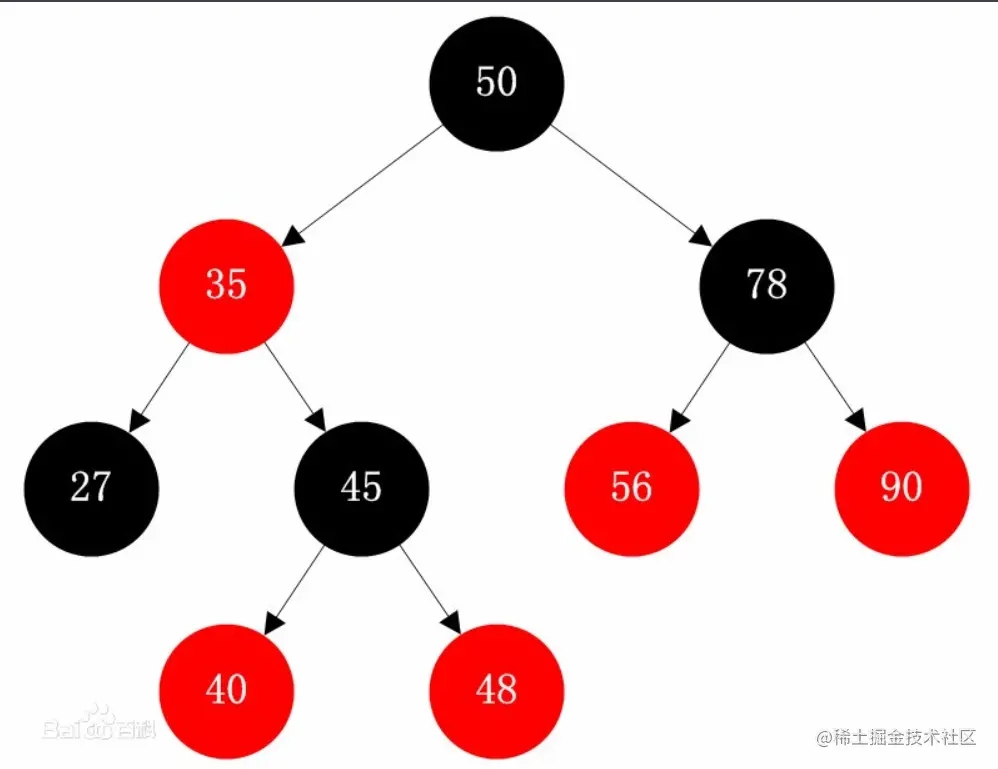
其内部的TreeMapEntry是它的结构体
static final class TreeMapEntry<K,V> implements Map.Entry<K,V> {
K key;
V value;
TreeMapEntry<K,V> left;
TreeMapEntry<K,V> right;
TreeMapEntry<K,V> parent;
boolean color = BLACK;
/**
* Make a new cell with given key, value, and parent, and with
* {@code null} child links, and BLACK color.
*/
TreeMapEntry(K key, V value, TreeMapEntry<K,V> parent) {
this.key = key;
this.value = value;
this.parent = parent;
}
/**
* Returns the key.
*
* @return the key
*/
public K getKey() {
return key;
}
/**
* Returns the value associated with the key.
*
* @return the value associated with the key
*/
public V getValue() {
return value;
}
/**
* Replaces the value currently associated with the key with the given
* value.
*
* @return the value associated with the key before this method was
* called
*/
public V setValue(V value) {
V oldValue = this.value;
this.value = value;
return oldValue;
}
public boolean equals(Object o) {
if (!(o instanceof Map.Entry))
return false;
Map.Entry<?,?> e = (Map.Entry<?,?>)o;
return valEquals(key,e.getKey()) && valEquals(value,e.getValue());
}
public int hashCode() {
int keyHash = (key==null ? 0 : key.hashCode());
int valueHash = (value==null ? 0 : value.hashCode());
return keyHash ^ valueHash;
}
public String toString() {
return key + "=" + value;
}
}
能看到除了key-value之外,还有left,right,parent表示左子节点,右子节点和父节点,还有一个boolean类型的color表示这个节点是红色的还是黑色的。也可以简单看看它的put方法
public V put(K key, V value) {
TreeMapEntry<K,V> t = root;
......
int cmp;
TreeMapEntry<K,V> parent;
// split comparator and comparable paths
Comparator<? super K> cpr = comparator;
if (cpr != null) {
do {
parent = t;
cmp = cpr.compare(key, t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
......
}
Comparator能实现自己的排序规则,一般都是默认的规则。通过compare去找到合适的位置插入红黑树,这段代码还是没什么难的地方,也不详细去讲了。
HashMap
这个相对而言就比较重要,因为用的比较多,所以可能会讲的相对更详细。可以先看看它的内部的数据结构,内部是一个节点数组Node<K,V>[] table,每个节点又是一个链表(或红黑树)的结构。
static class Node<K,V> implements Map.Entry<K,V> {
final int hash;
final K key;
V value;
Node<K,V> next;
Node(int hash, K key, V value, Node<K,V> next) {
this.hash = hash;
this.key = key;
this.value = value;
this.next = next;
}
public final K getKey() { return key; }
public final V getValue() { return value; }
public final String toString() { return key + "=" + value; }
public final int hashCode() {
return Objects.hashCode(key) ^ Objects.hashCode(value);
}
public final V setValue(V newValue) {
V oldValue = value;
value = newValue;
return oldValue;
}
public final boolean equals(Object o) {
if (o == this)
return true;
if (o instanceof Map.Entry) {
Map.Entry<?,?> e = (Map.Entry<?,?>)o;
if (Objects.equals(key, e.getKey()) &&
Objects.equals(value, e.getValue()))
return true;
}
return false;
}
}
节点主要有3个重要的参数,key,value和key的hash。
那我们就先需要搞懂它的一个逻辑,它会想用Key去生成hash,再用hash去计算出这个节点在数组中的下标。所以先看计算key的hash的方法
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
拿到key的hashcode,然后让这个hashcode的高16位和低16位做异或运算。这个操作是为了什么呢?这个是为了降低哈希冲突的概率,那这里又引出了什么是hash冲突?
这里直接说会比较难去理解,没关系,我们先往下讲如何通过hash去计算数组的位置,理解完这个步骤之后我们再反回来讲哈希冲突这个事。
在HashMap的put方法中有一段代码
......
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
......
这个(n - 1) & hash就是计算数组下标的方式,通过hash和数组长度-1做与运算,来得到这个节点应该插入到数组的哪个位置。那为何要用hash和数组长度-1做与运算,这个数组长度-1是什么东西?这又要涉及到另一个知识点,所以说hashmap中的细节比较多。
首先这个hashmap的长度,必须是2的n次方,比如4,8,16,32。 它内次扩容也是x2,这时候我们再去看长度-1,比如长度是16,那16-1是15,它对应的二进制是1111,假如长度是32,那31的二进制是11111。看到这里相信你已经知道长度-1代表什么了。讲到长度,这里又会涉及一个知识点是为什么HashMap的默认长度是16,定8不行吗?定32不行吗?这个放到最后讲。
我们回过来先继续去说哈希冲突这事,什么是哈希冲突?hash冲突的意思是两个不同的对象,计算出来的哈希值相同。放在HashMap中你也可以简单理解成,两个不同的key计算出的数组下标相同。而HashMap中解决哈希冲突的方法是上面的高16位和低16位做异或,和用链地址法(就是相同的话,节点用链表或者红黑树表示)
链地址法比较容易理解,主要还是为什么hash的高16位和低16位做异或能降低哈希冲突的概率。那是因为平常计算的时候,高16位是不会参与计算的, 我举个例子,假如两个不同的key计算出来的hash值,高16位不同,低16位相同,数组长度是16,这时候你这两个hash与15做与运算,得到的结果相同吧,那不就冲突了?如果我把高16位和低16位先做异或,这时候会让高16位参与到运算中,所以他们计算出的结果就会不同。
此时可能有人会想,那为什么不把32位的hash分4段做异或,4段8位做异或,这样不就更充分吗?这样确实能更先降低数组长度是16情况下的哈希冲突概率,但是你要考虑整形的最大值,当数组的长度-1达到16位时,这样做就会出现问题。
通过Key计算出数组的位置,如果这个位置没节点,就把这个节点放入,如果有节点,就遍历这个节点的链表,所以我们看put方法具体的操作
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
// 判断数组中没结点的话创建结点然后添加进取
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
else {
Node<K,V> e; K k;
// 判断结点的hash和key是相等的话直接改值
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
e = p;
else if (p instanceof TreeNode)
// 判断是红黑树的情况(后面会说)
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
else {
// 判断是链表的情况,循环遍历链表找到hash和key相同的结点
for (int binCount = 0; ; ++binCount) {
if ((e = p.next) == null) {
// 没找到的情况下创建一个新的结点放到链表末尾
p.next = newNode(hash, key, value, null);
// 判断是否需要将链表转成红黑树
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
treeifyBin(tab, hash);
break;
}
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
break;
p = e;
}
}
// 找到相同的key,直接替换value然后结束流程
if (e != null) { // existing mapping for key
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}
}
++modCount;
// 扩容
if (++size > threshold)
resize();
// 钩子
afterNodeInsertion(evict);
return null;
}
从中能看出put内部的主要操作是判断对应数组的位置是否有结点,没有的话直接放进去,有的话遍历这个结点的链表或者红黑树,找到hash和key相同的结点替换掉,如果没有,则新建结点放到尾部,如果链表的长度到达8,将链表转成红黑树。最后再判断是否要扩容。
这段代码还是比较容易理解的,先讲讲最后的afterNodeInsertion,钩子函数,虽然在这里面没有任何代码,但从设计的角度去看,这是一个比较好的设计,可以增强扩展性。
比较重要的操作就是转红黑树的操作,可以看看它的常量定义
/** * The bin count threshold for using a tree rather than list for a * bin. Bins are converted to trees when adding an element to a * bin with at least this many nodes. The value must be greater * than 2 and should be at least 8 to mesh with assumptions in * tree removal about conversion back to plain bins upon * shrinkage. */ static final int TREEIFY_THRESHOLD = 8; /** * The bin count threshold for untreeifying a (split) bin during a * resize operation. Should be less than TREEIFY_THRESHOLD, and at * most 6 to mesh with shrinkage detection under removal. */ static final int UNTREEIFY_THRESHOLD = 6;
可以看到这里小于6个的时候转回链表,转的操作在resize的split方法。说到resize,我们也可以看看,这个方法也算重点
final Node<K,V>[] resize() {
Node<K,V>[] oldTab = table;
int oldCap = (oldTab == null) ? 0 : oldTab.length;
......
int newCap, newThr = 0;
if (oldCap > 0) {
......
// 重点是newCap = oldCap << 1
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
oldCap >= DEFAULT_INITIAL_CAPACITY)
......
}
......
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
table = newTab;
if (oldTab != null) {
for (int j = 0; j < oldCap; ++j) {
Node<K,V> e;
if ((e = oldTab[j]) != null) {
oldTab[j] = null;
if (e.next == null)
// 单结点情况下的扩容
newTab[e.hash & (newCap - 1)] = e;
else if (e instanceof TreeNode)
// 红黑树情况下的扩容
((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
else { // preserve order
// 链表情况下的扩容
Node<K,V> loHead = null, loTail = null;
Node<K,V> hiHead = null, hiTail = null;
Node<K,V> next;
do {
next = e.next;
if ((e.hash & oldCap) == 0) {
if (loTail == null)
loHead = e;
else
loTail.next = e;
loTail = e;
}
else {
if (hiTail == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
}
} while ((e = next) != null);
if (loTail != null) {
loTail.next = null;
newTab[j] = loHead;
}
if (hiTail != null) {
hiTail.next = null;
newTab[j + oldCap] = hiHead;
}
}
}
}
}
return newTab;
}
我这里屏蔽了一些代码,只保留重点的代码,能简单的看出扩容的操作就是创建另一个数组,然后给新数组赋值后覆盖旧数组。如果看过上一篇文章的ArrayList,那就能很容易知道,短时间频繁的扩容会导致内存抖动,所以为什么初始长度不定2,不定4,不定8 。然后看最主要的扩容操作newCap = oldCap << 1,新的长度是旧的长度左移动一位,其实就是x2,所以上面有说hashmap的长度都是2的n次方。
然后看看3种不同情况的扩容,先看单结点的情况,如果数组中对应的位置只有一个结点,那就重新计算它的下标,然后换个位置。
再先看如果是链表的情况。它会把链表拆分成两条链表,分别放到数组的newTab[j]和newTab[j + oldCap] ,这个大概的思路是这样,详细的话多看几次代码也能很容易理解。最后再来看红黑树的情况。调用split方法
final void split(HashMap<K,V> map, Node<K,V>[] tab, int index, int bit) {
TreeNode<K,V> b = this;
// Relink into lo and hi lists, preserving order
TreeNode<K,V> loHead = null, loTail = null;
TreeNode<K,V> hiHead = null, hiTail = null;
int lc = 0, hc = 0;
for (TreeNode<K,V> e = b, next; e != null; e = next) {
next = (TreeNode<K,V>)e.next;
e.next = null;
if ((e.hash & bit) == 0) {
if ((e.prev = loTail) == null)
loHead = e;
else
loTail.next = e;
loTail = e;
++lc;
}
else {
if ((e.prev = hiTail) == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
++hc;
}
}
if (loHead != null) {
if (lc <= UNTREEIFY_THRESHOLD)
tab[index] = loHead.untreeify(map);
else {
tab[index] = loHead;
if (hiHead != null) // (else is already treeified)
loHead.treeify(tab);
}
}
if (hiHead != null) {
if (hc <= UNTREEIFY_THRESHOLD)
tab[index + bit] = hiHead.untreeify(map);
else {
tab[index + bit] = hiHead;
if (loHead != null)
hiHead.treeify(tab);
}
}
}
这里只需要简单理解,TreeNode这个数据结构是继承Node的,for循环中的操作其实就和链表中的操作一样,分成low和height两部分,然后判断小于UNTREEIFY_THRESHOLD也就是6的情况下,转成Node结点,也就是树转回链表。
总结
这次主要讲了ArrayMap、TreeMap和HashMap3个数据结构,因为这3个用得比较多,但并不是Map中只有这3个,比如Map中还有IdentityHashMap、WeakHashMap这些,但是比较常用的就是这3种,其中最重要的是HashMap。
HashMap中比较重要的是它的一些设计的思想,比如如何去解决和降低哈希冲突,为什么默认的大小是16,其次要了解它的一个工作原理,我这里主要是以put方法来举例,当中就涉及到像链地址法,链表转红黑树,扩容等操作。和LinkedList一样,我也十分建议没看过HashMap源码的人能去看看,体验一下它内部的一些代码设计思想和细节的处理。
通过这两篇文章,平常比较常用的数据结构基本都讲完了,下一篇就开始讲讲和线程安全相关的数据结构。
以上就是Android Map数据结构全面总结分析的详细内容,更多关于Android Map数据结构的资料请关注脚本之家其它相关文章!
