Java 十大排序算法之计数排序刨析
作者:龍弟-idea
计数排序是一个非基于比较的排序算法,该算法于1954年由 Harold H. Seward 提出。它的优势在于在对一定范围内的整数排序时,它的复杂度为Ο(n+k)(其中k是整数的范围),快于任何比较排序算法
计数排序是非比较的排序算法,用辅助数组对数组中出现的数字计数,元素转下标,下标转元素
计数排序优缺点
优点:快
缺点:数据范围很大,比较稀疏,会导致辅助空间很大,造成空间的浪费
使用范围:数据较为密集或范围较小时适用。
思路
1.找出最大元素max

2.初始化一个max+1的数组

3.将每个元素的计数存储在数组中各自的索引处

4.存储计数数组元素的累积和

5.数组中找到原始数组的每个元素的索引
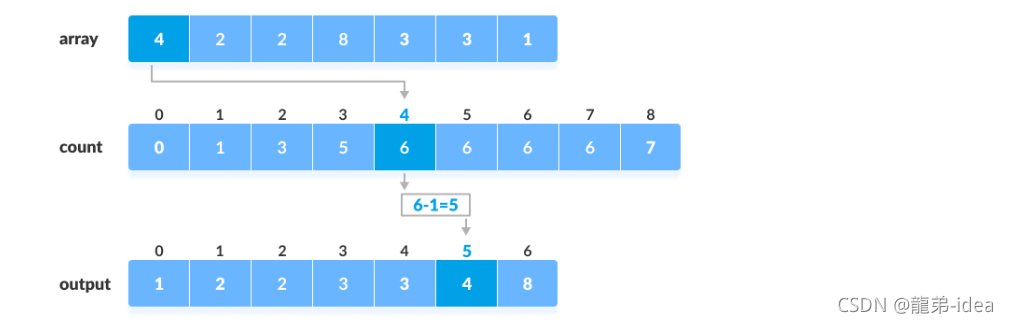
计数排序代码实现
public class CountingSort {
private static int[] countingSort(int[] arr) {
//1、求取最大值和最小值,计算中间数组的长度:中间数组是用来记录原始数据中每个值出现的频率
int min = arr[0], max = arr[0];
for (int i : arr) {
if (i > max) {
max = i;
}
if (i < min) {
min = i;
}
}
//2、有了最大值和最小值能够确定中间数组的长度
//例如存储 5-0+1=6
int[] countArray = new int[max - min + 1];
//3、循环遍历旧数组计数排序: 就是统计原始数组值出现的频率到中间数组B中
for (int i : arr) {
countArray[i - min] += 1; //数的位置上+1
}
//4、统计数组做变形,后边的元素等于前面的元素之和
for (int i = 1; i < countArray.length; i++) {
countArray[i] += countArray[i - 1];
}
//5、倒序遍历原始数组,从统计数组中找到正确的位置,输出到结果数组
int[] resultArray = new int[arr.length];
for (int i = arr.length - 1; i >= 0; i--) {
//给resultArray的当前位置赋值
resultArray[countArray[arr[i] - min] - 1] = arr[i];
//给countArray的位置的值--
countArray[arr[i] - min]--;
}
return resultArray;
}
public static void main(String[] args) {
int[] arr = {1,28,3,21,11,7,6,18};
int[] sortedArr = countingSort(arr);
System.out.println(Arrays.toString(sortedArr));
}
}
时间复杂度:O(n+k)
到此这篇关于Java 十大排序算法之计数排序刨析的文章就介绍到这了,更多相关Java 计数排序内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家!
