详解Python中递归函数的原理与使用
作者:小小垂髫
什么是递归函数
如果一个函数,可以自己调用自己,那么这个函数就是一个递归函数。
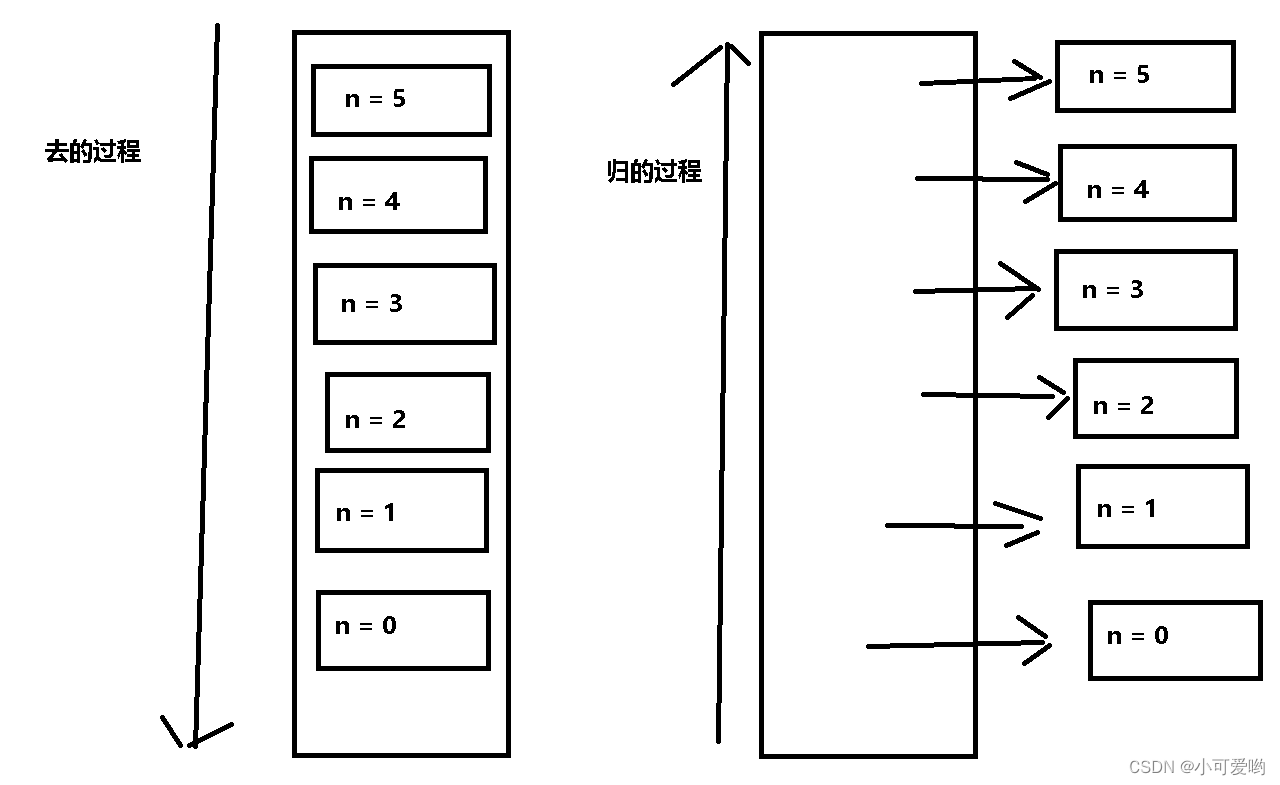
递归,递就是去,归就是回,递归就是一去一回的过程。
递归函数的条件
一般来说,递归需要边界条件,整个递归的结构中要有递归前进段和递归返回段。当边界条件不满足,递归前进,反之递归返回。就是说递归函数一定需要有边界条件来控制递归函数的前进和返回。
定义一个简单的递归函数
# 定义一个函数
def recursion(num):
print(num)
if num == 0:
return 'ok'
# 这个函数在自己的作用域中调用自己,这个函数就是一个递归函数
recursion(num-1)
recursion(10)
"""
结果:
10
9
8
7
6
5
4
3
2
1
0
"""
代码解析
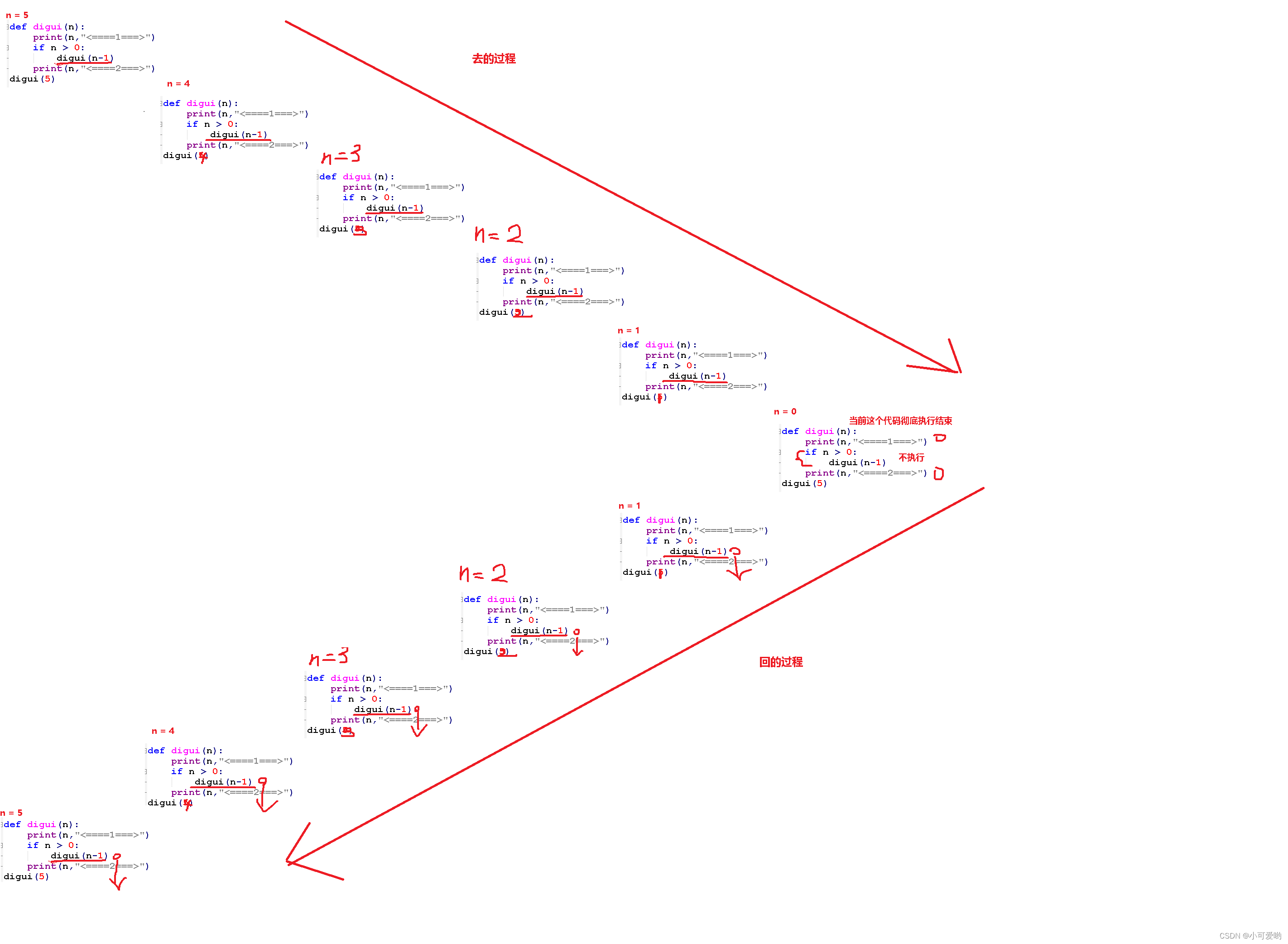
我们执行这个函数,参数给了一个10,但是这个函数执行的过程中,又调用了自己,所以现在这个函数就会进入先执行第二次调用自己的过程中,第一次的调用就暂时的阻断了;
第二次调用的时候,num-1,参数就变成了9,继续执行,然后就又执行到了调用自己的代码中,现在就会执行第三次调用的过程中,第二次的调用也阻断了;
这就是 递 的过程;
…………
第十一次调用的时候,num-1,层层的嵌套,参数就变成了0,就符合了作用域中的if num == 0的条件判断式,第十一次的调用就没有再执行到了调用自己的代码,而是彻彻底底的执行完成了 ,然后代码的执行就又回到了第十次的函数调用中。
第十次的函数调用阻断的时候是执行到了recursion(num-1),但是这一行代码执行完了,也就是第十一次调用执行完了,并且后面也没有任何代码,所以第十次调用也结束了,然后就回到了第九次调用;然后第八次;再就是第七次,一直到第一次结束,整个函数的执行就结束了;
这就是 归 的过程。
内存栈区堆区
栈区空间就是我们常说的栈,栈是一个有去有回,先进后出后出的空间,就像我们上面的例子中讲的,我们最先执行的是函数的第一次调用,但是第一次调用却是最后执行释放掉的,而第十一次调用是最后调用,最先执行释放掉的,这就是先进后出。与栈空间概念相违背的是队列空间,队列空间是一个有去有回,先进先出的空间,就像我们平时排队一样,先排队的会比后来的人先买到票,之后我们学习并发的时候,我们会详细的讲述队列的概念。
单独的讲栈堆就是一种数据结构,栈是先进后出的一种数据结构,堆是排序后的一种树状数据结构。
栈区堆区是内存空间,栈区就是按照先进后出的数据结构,无论创建或销毁都是自动为数据分配内存,释放内存,这是系统自动创建的;堆区就是按照排序后的树状数据结构,可优先取出必要的数据,无论创建或者销毁都是手动分配内存,释放内存,这是编程工作者手动编程出来的。
| 内存空间 | 特点 |
|---|---|
| 内存中的栈区 | 自动分配,自动释放 |
| 内存中的堆区 | 手动分配,手动释放 |
运行程序时在内存中执行,会因为数据类型的不同而在内存的不同区域运行,因不同语言对内存划分的机制不一,当大体来说,有如下四大区域:
- 栈区:分配局部变量空间;
- 堆区:是用于手动分配程序员申请的内存空间;
- 静态区:又称之为全局栈区,分配静态变量,全局变量空间;
- 代码区:又称之为只读区、常量区,分配常量和程序代码空间;
上面的栈区、读取、静态区、代码区都只是内存中的一段空间。
死递归
所以我们在使用递归函数的时候要注意,递归函数调用的过程就是一个开辟栈和释放栈的过程,调用的时候开辟栈空间,结束的时候释放栈空间,所以说,如果开辟的空间不结束就会一直存在,就会一直占用内存空间,但是栈空间是一个先进后出的空间,如果新开启的空间不释放掉,之前的空间也不会释放掉的,那么如果我们开辟的空间很多很多,但是又释放不掉,那么我们弱小的内存是否有足够的空间容纳得下这么多的栈呢?如果容纳不下,那么我们的计算机就会爆炸,所以我们在使用递归的时候要注意避免这种情况。尤其是死递归。
每次调用函数时,在内存宗都会单独开辟一个空间,配合函数运行,这个空间叫做栈帧空间。
1、递归是一去一回的过程,调用函数时,会开辟栈帧空间,函数执行结束之后,会释放栈帧空间,递归实际上就是不停地开辟和释放栈帧空间的过程,每次开辟栈帧空间,都是独立的一份,其中的资源不共享。
2、触发回的过程当最后一层栈帧空间全部执行结束的时候,会触底反弹,回到上一层空间的调用处,遇到return,会触底反弹,回到上一层的调用处
3、写递归时,必须给予递归跳出的条件,否则会发生内存溢出,可能会出现死机的情况,所以当递归的层数过多的时候,不建议使用递归。
Python中的环境递归的层数默认为1000层左右,一般都是996层。
# 下面的递归函数没有跳出递归的条件,所以是一个死递归,执行看,是不是1000左右。 def recursion(num): print(num) recursion(num+1) recursion(1)
尾递归
简单的来说,在函数返回的时候,调用其本身,并且return语句不包含表达式,这样的一个递归函数就是一个尾递归函数。
换句话说返回的东西就是函数本身就是尾递归函数,而递归函数只是自身调用了自身而已。
一般情况下,尾递归的计算在参数中完成。
我们开始的举例是一个尾递归函数吗?不是,因为那个例子这是调用了自己本省,但是并没有返回,所以还是一个普通的递归函数而已。
使用递归的时候,我们通常在一些技术博客上看到一些关于尾递归优化的东西,这是因为尾递归无论调用多少次函数,都只会占用一份空间,只开辟一个栈帧空间,但是目前 cpython 不支持,然而最常见的解释器就是 cpython 。
Python常见的解释器:cpython、pypy、jpython。
尾递归相比普通递归的优点就是返回值不需要额外过多的运算。
实例
阶乘计算
一个正整数的阶乘是所有小于及等于该数的正整数的积,并且0的阶乘为1。
""" 循环计算 """
def factorial(num):
if num == 0:
return 1
elif num < -1:
return '只能是零和正整数'
count = 1
for i in range(1, num+1):
count *= i
return count
res = factorial(5)
print(res) # 120
""" 使用普通递归 """
def factorial(num):
if num == 0:
return 1
elif num < -1:
return '只能是零和正整数'
elif num == 1:
return num
return num * factorial(num-1) # 普通函数返回的是一个表达式
res = factorial(5)
print(res) # 120
""" 使用尾递归 """
def factorial(num, count=1):
if num == 0:
return 1
elif num < -1:
return '只能是零和正整数'
elif num == 1:
return count
return factorial(num-1, count*num) # 尾递归返回的是一个函数,计算式在参数中运算
res = factorial(5)
print(res) # 120
斐波那契数列
斐波那契数列是以0、1两个数开头,从这个数列从第3个数开始,每一个数都等于前两树之和。
# 使用循环解决
def fibonacci(num):
x, y = 0, 1
if num < 1:
return '输入大于0的数字'
elif num == 1:
return 0
elif num == 2:
return 1
for _ in range(num-2):
x, y = y, y+x
return y
res = fibonacci(9)
print(res) # 21
""" 使用普通递归 """
def fibonacci(num):
if num < 1:
return '输入大于0的数字'
elif num == 1:
return 0
elif num == 2:
return 1
return fibonacci(num-1) + fibonacci(num-2)
res = fibonacci(9)
print(res) # 21
""" 使用尾递归 """
def fibonacci(num, x=0, y=1):
if num < 1:
return '输入大于0的数字'
elif num == 1:
return x
elif num == 2:
return y
return fibonacci(num-1, x=y, y=(x+y))
res = fibonacci(9)
print(res) # 21到此这篇关于详解Python中递归函数的原理与使用的文章就介绍到这了,更多相关Python递归函数内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家!
