JavaScript

关注公众号 jb51net

关闭
首页 > 网络编程 > JavaScript > JS前端canvas手势识别

JS前端使用canvas搞一个手势识别

作者：尤水就下

这篇文章主要为大家介绍了JS前端使用canvas搞一个手势识别的实现示例详解，有需要的朋友可以借鉴参考下，希望能够有所帮助，祝大家多多进步，早日升职加薪

前言

最近在看一些关于图形学的东西，写了个一笔画手势识别的小 demo，效果大概是下面这个样子：

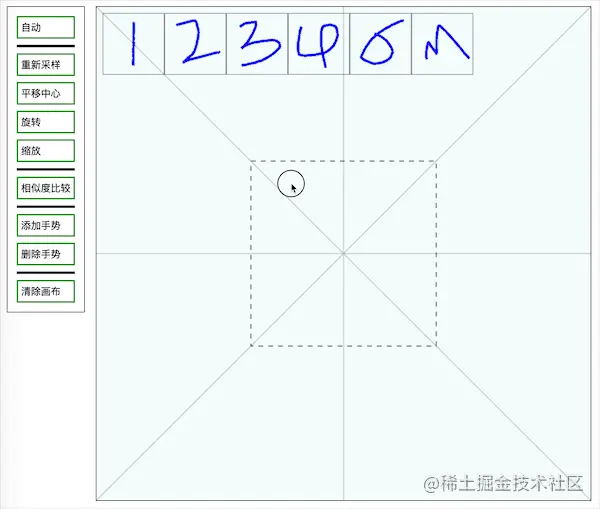
如果你是初次看过肯定会觉得很有意思🤩。哈哈，话不多说，让我们直接开撸吧。

这里可以先花几秒钟想一下你会怎么做🤔？带着问题往下看能够记得更牢固，比如你可能最关心的就是怎么识别怎么对比。这里先提前贴上项目 demo 地址，有需要的自取。另外这里并不会涉及什么人工智能、AI识别、深度学习啥的，所以请放心食用🍚。

具体步骤

发车啦 🏎💨💨💨

第一步：手势绘制

既然要识别那肯定得先有手势啦，所以第一步要做的就是手势绘制，这一步相对来说比较简单，学习过 canvas 的同学应该有看过画板的实现，这个也是一样的，监听 canvas 上的鼠标事件，然后在移动的时候将鼠标坐标点用线段相连即可，不同的是我们在绘制过程中还顺便把每个坐标点都画了一下，核心代码如下（可跳过）：

handleMousemove(e: MouseEvent) {
    if (!this.isMove) return;
    const curPoint = this.getCanvasPos(e);
    const lastPoint = this.inputPoints[this.inputPoints.length - 1];
    // 画线段
    CanvasUtils.drawLine(this.ctx2d, lastPoint[0], lastPoint[1], curPoint[0], curPoint[1], 'blue', 3);
    // 画坐标点
    CanvasUtils.drawCircle(this.ctx2d, curPoint[0], curPoint[1], 5);
    // 如果觉得原始点的数量太多，可以节流
    this.inputPoints.push(curPoint);
}

画完之后大概是下面这个样子：

从上图可以看到绘制出来的红点并不均匀，因为一笔画过程中的手速不一样，疏密程度也就不一样，所以为了避免这个因素的影响，我们需要重新取个样。

第二步：重新取样

不同场景的取样方式也有所不同。这里我们简单的选择等分线条取样即可，也就是先计算出整个手势的长度（所有线段长度相加），然后 n 等分取点（随便几等分，看效果调节，不用纠结）。

注意我们并没有改变原始坐标点的信息，手势的绘制还是要按照原来的点绘制，所以需要加一个变量来存储新采样的点（后面的计算全都是用新的取样点来计算）。这个计算还是有点小麻烦的，所以我准备了一张图方便大家理解👇🏻：

然后就是具体的代码实现（大概懂了可跳过）：

export type Point = [number, number];
static resample(inputPoints: Point[], sampleCount: number): Point[] {
    const len = GeoUtils.getLength(inputPoints);
    const unit = len / (sampleCount - 1);
    const outputPoints: Point[] = [[...inputPoints[0]]];
    let curLen = 0;
    let prevPoint = inputPoints[0];
    for (let i = 1; i < inputPoints.length; i++) {
        const curPoint = inputPoints[i];
        let dx = curPoint[0] - prevPoint[0];
        let dy = curPoint[1] - prevPoint[1];
        let tempLen = GeoUtils.getLength([prevPoint, curPoint]);
        while (curLen + tempLen >= unit) {
            const ds = unit - curLen;
            const ratio = ds / tempLen;
            const newPoint: Point = [prevPoint[0] + dx * ratio, prevPoint[1] + dy * ratio];
            outputPoints.push(newPoint);
            curLen = 0;
            prevPoint = newPoint;
            dx = curPoint[0] - prevPoint[0];
            dy = curPoint[1] - prevPoint[1];
            tempLen = GeoUtils.getLength([prevPoint, curPoint]);
        }
        prevPoint = curPoint;
        curLen += tempLen;
    }
    while (outputPoints.length < sampleCount) {
        outputPoints.push([...prevPoint]);
    }
    return outputPoints;
}

重新采样之后大概是下面这个效果：

要注意如果你采用了 n 等分，那么所有的手势都应该是 n 等分的，不能改变，否则难以比较。另外我们顺便把手势的中心点算了出来（就是简单的把每个采样点坐标相加取平均值），并且将手势的起始点（最后一个点也行）与中心点相连，这个你可以粗浅的认为它表示的是这个手势的大致方向，不理解可以先跳过，后续会讲到。

第二步：平移

其实你要比较任何东西，都是要量化成数字来比较的，而不是通过感觉。 不能说我觉的两个手势长得像它就像，那只是人工没有智能，所以我们要怎么解决这个问题呢？我们需要定一个标准，让所有手势都在同一个模子下进行比较（就好像你要找个对象，不得有个衡量标准吗），比如都变成同样的大小、同样的方向。

不然你想想如果我竖着写了一个很大的3和横着写了一个很小的3，它们要怎么比较。所以接下来我们要做的就是把手势标准化（其实每幅示例图中的虚线框就是我们的架子），为后续的比较打好基础，为此就需要经历平移、旋转、缩放这几个步骤。

关于平移，刚才我们已经计算过手势的中心点，现在只需要把它移动到画布中心即可，简单算下平移距离，然后对所有新的采样点做平移操作即可，示例代码如下：

// 对每个坐标点进行平移
static translate(points: Point[], dx: number, dy: number) {
    points.forEach((p) => {
        p[0] += dx;
        p[1] += dy;
    });
}

效果如下：

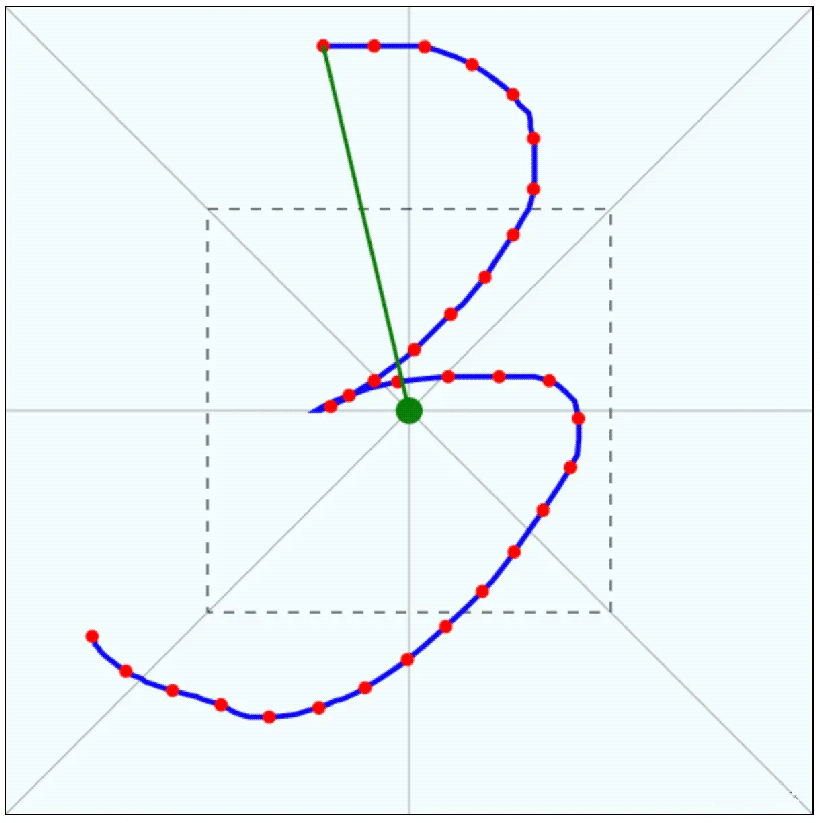
要注意我们在绘制的时候需要将画布左上角的原点移到到画布中间，这样做能够极大的方便计算，包括接下来的旋转和缩放也是在平移坐标系的基础上。

第三步：旋转

细心的同学会发现除了中间的虚线框，我们还把整个画布八等分了，这是为什么呢？其实上文中有提到，是因为手势具有方向性，比如 丨和 /，这两种手势本应该很相近，但是方向不同，所以就需要进行一定的旋转。

而这里的八条等分线就是我们要靠近的方向（几等分也是你自己随意取的），于是乎我们可以简单地算下手势方向（图中的绿线）离哪条等分线近就往哪边旋转，然后把所有的点都进行旋转变换即可，代码如下（可跳过）：

// 计算需要旋转到最近辅助线的弧度，center 为中心点，startPoint 为手势起始点，sublineCount 为坐标等分数量
static computeRadianToSubline(center: Point, startPoint: Point, sublineCount: number): number {
    const dy = startPoint[1] - center[1];
    const dx = startPoint[0] - center[0];
    let radian = Math.atan2(dy, dx);
    if (radian < 0) radian += TWO_PI;
    const unitRadian = TWO_PI / sublineCount;
    const targetRadian = Math.round(radian / unitRadian) * unitRadian;
    radian -= targetRadian;
    return radian;
}
// 对每个坐标点进行旋转
static rotate(points: Point[], radian: number) {
    const sin = Math.sin(radian);
    const cos = Math.cos(radian);
    points.forEach((p) => {
        let [x, y] = p;
        p[0] = cos * x - sin * y;
        p[1] = sin * x + cos * y;
    });
}

很多同学可能会觉得旋转比平移难，其实很简单的，你只需要知道一个点是怎么旋转的就行了（线段的旋转就是两个端点的旋转，多边形的旋转就是多个顶点的旋转），这里我画了张推导图方便大家理解（不感兴趣也可以跳过）：

然后看下这步的效果图：

第四步：缩放

我们每次绘制的手势是有大有小的，所以这里需要统一成一个大小，也就是做个缩放。

比如我们要把一个 600*600 的手势放进一个 100*100 的容器中（也就是图中的虚线框），那就要缩小 6 倍。

那具体要怎么求呢？首先我们要求出手势的包围盒大小，这里采用AABB模型（还有OBB、球模型等）。

那什么是 AABB 包围盒呢，这个贼简单，就是找出所有采样点的最大最小 x、y 值即可，就像下面这样：

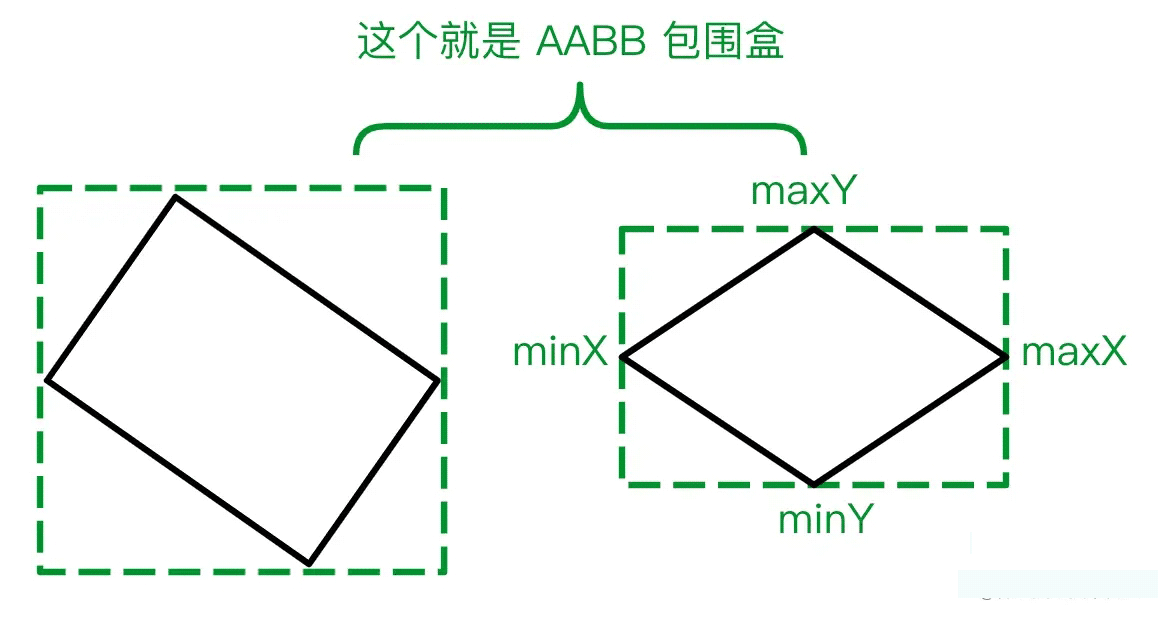
现在只要用容器长度除以 AABB 的最长边，得到的就是缩放倍数。然后同样的，遍历所有点进行缩放操作，具体代码如下：

// 再次提醒下因为我们已经把坐标系移到了画布中央，画布中心和手势中心是重合的，所以直接乘以缩放倍速就可以了
static scale(points: Point[], scale: number) {
    points.forEach((p) => {
        let [x, y] = p;
        p[0] = x * scale;
        p[1] = y * scale;
    });
}

效果图如下：

注意不是说缩放之后的图形一定要在虚线框里面，而是缩放之后的图形大小和虚线框差不多。

第五步：手势录入

这个就是简单的保存数据，一共可分为两步：

第六步：比较（重点）

假设我们已经有了两个标准化后的手势，那怎样才能知道他们相似呢？如果你没看过相关知识，大概率是不懂的，我。也是😂。。。同样的，这里也可以停下来思考几秒种🤔。。。 ok，其实手势相似与否可以转成两组采样点是否足够靠近的问题，一种直观的解法就是计算两组采样点之间的距离，看是否小于某个阈值，类似下面这样：

不懂的话想成一个采样点就好理解了（就变成了求两点距离🐶），具体代码如下：

static squaredEuclideanDistance(points1, points2) {
    let squaredDistance = 0;
    const count = points1.length;
    for (let i = 0; i < count; i++) {
        const p1 = points1[i];
        const p2 = points2[i];
        const dx = p1[0] - p2[0];
        const dy = p1[1] - p2[1];
        squaredDistance += dx * dx + dy * dy;
    }
    return squaredDistance;
}

其实上面这种方法有个高大上的名字，叫欧氏距离（好了好了，别装了😂）。

但是对于我们这种场景有个更好的相似度算法（算法？溜了溜了！），所以接下来我们来介绍一个余弦相似度的概念（不难的，我都画了图的，包看包会）：

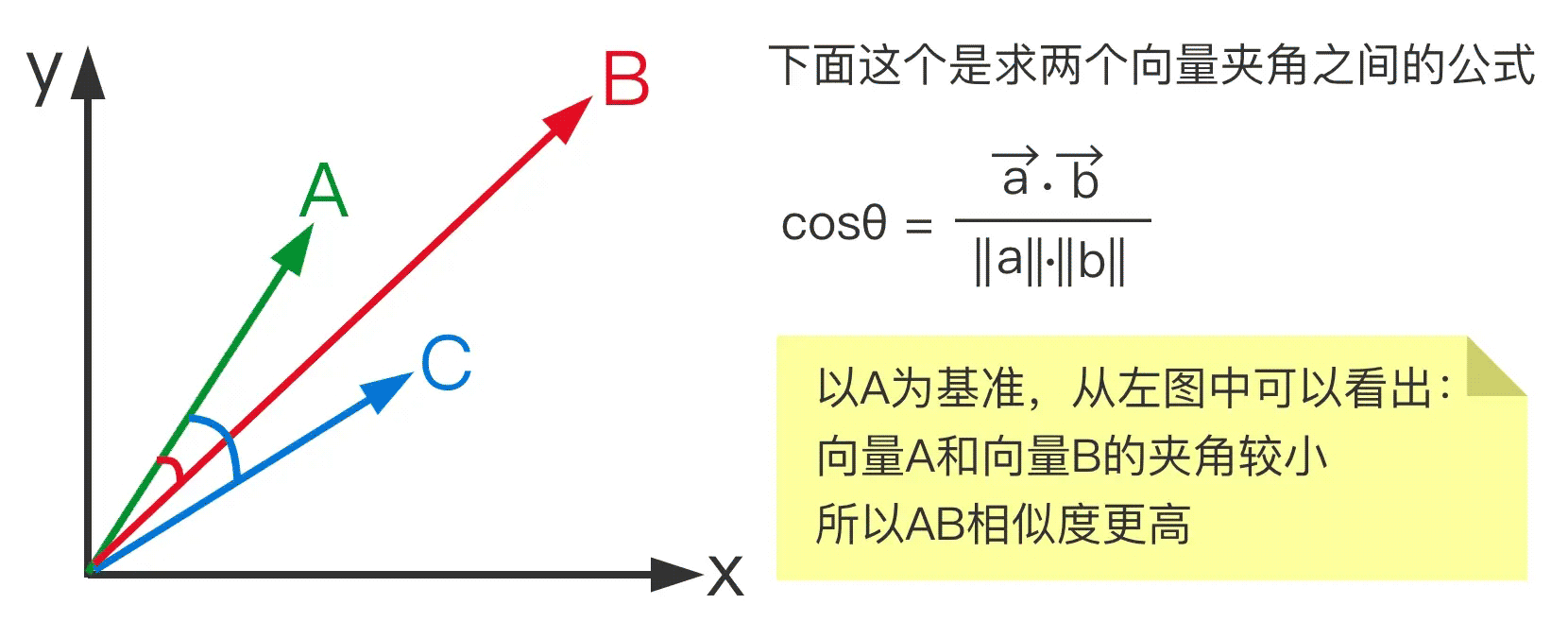
如果上图采用的是欧氏距离比较，显然 AC 距离更近更相似。

如果用余弦值比较，那显然是 AB 更相似。

这是因为欧氏距离得到的是绝对差异，余弦相似度比较的是相对差异（仔细品品🍚）。

那为什么夹角的大小可以判定两点的相似度呢？

其实这个方法主要判定的是两点方向的相似度，你可以看到即便向量B很长，但是不影响它的方向朝向，所以B的目标朝向和A更相近，这个用力学的知识会比较好理解一点，看下下面这张图：

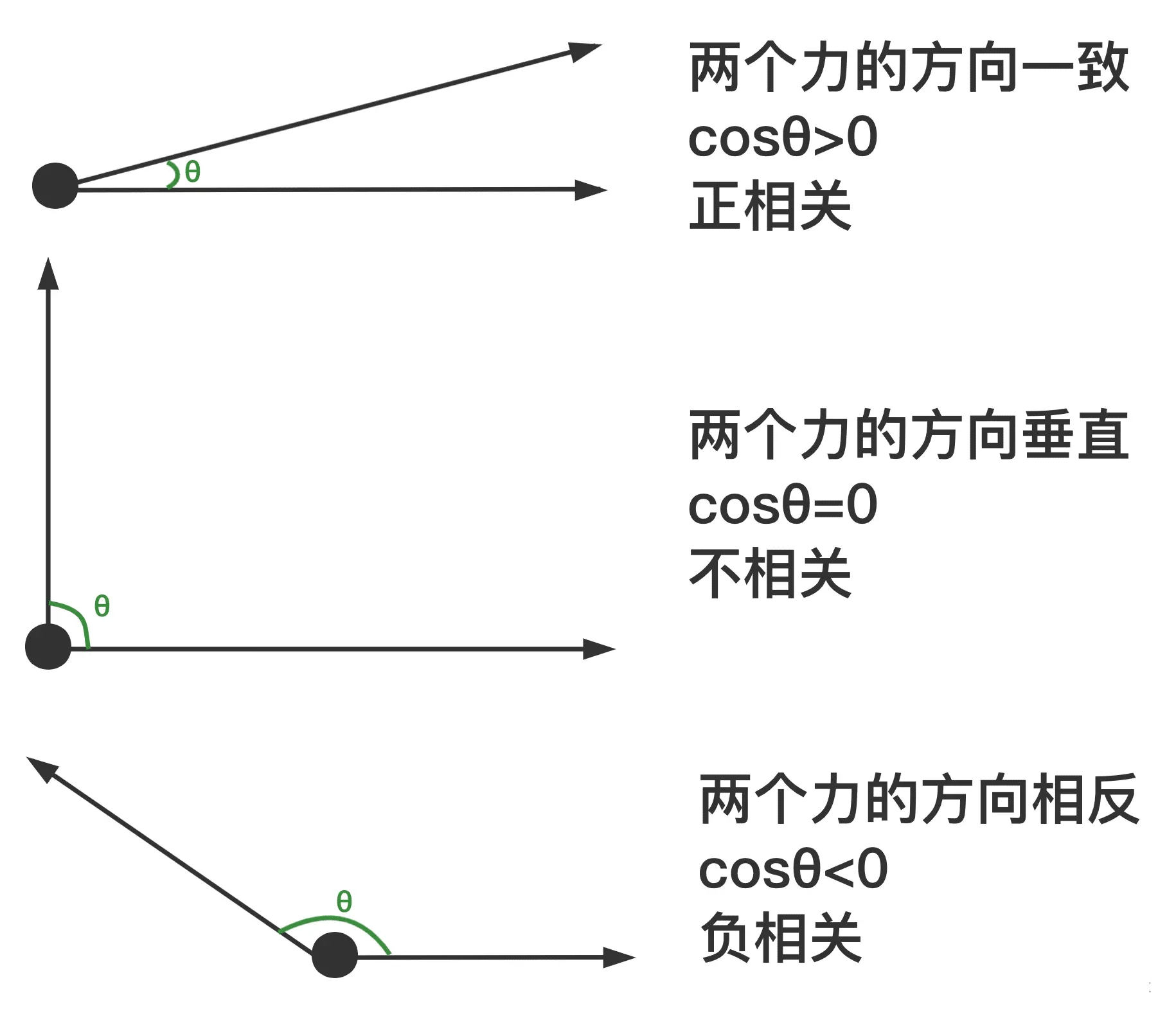
夹角越小，发力的方向才越一致，我们才能拉动一个物体（我们就是有相同目标的一类人，也就是相似）。那这么多个点我们怎么算余弦相似度呢？

回头看看刚才求夹角的公式，既然只和方向相关，而和向量A、向量B长度无关，那么我们一般可以把A、B变成单位向量（就是向量除以它们自身的长度），这样A、B的模长就为1，于是余弦值就可以变成这样：

是不是突然简单了不少，接下来我们就想办法把手势变成向量就行（就是变成一个很长的数组），这里看图理解会方便些：

我们可以把转变后的一维数组叫做这个手势的特征，并当做数据保存下来，下次比较的时候直接把这个数组拿出来算余弦值即可。

// 计算余弦相似度
static calcCosDistance(vector1: number[], vector2: number[]): number {
    let similarity = 0;
    vector1.forEach((v1, i) => {
        const v2 = vector2[i];
        similarity += v1 * v2;
    });
    return similarity; // 相似度介于 -1~1
}

余弦相似度在很多场合都是有用到的，比如文章相似度中词向量的应用（扯远了），所以这里简要回顾一下它的具体思路：

注意事项

比较的基本套路（可跳过）

这里简单补充下比较两个东西是否相似的一般套路，也就两大步：

特征提取（就是处理数据的过程）：

不管是什么东西，都有对应的原始数据，我们要做的就是将其（经过层层处理）转换成同一个框架维度下（也就是标准化），通常就是将原始数据转换成长度相同的一维数组（再次强调虽然是一维数组，但其实是 n 维向量）。

算法识别（就是比较数据的过程）：

我们以一个极其简单的推荐算法为例，推荐算法的问题在某种程度上可以转换成两个人的喜好相似程度：

喜好干饭摸鱼睡觉就是玩...
甲（咸鱼）✅✅✅✅...
乙（翻身）❌❌❌❌...
我✅?✅?...

这个和我们的手势识别不能说是很像，只能说是一模一样，在已有的手势中（甲乙）找一个和我（喜好）相似度较高的，每一行其实就是一系列采样点，最终可以简单的推断出我（可能）是条咸鱼😂，还喜欢摸鱼。

又比如你打算买一台电脑，那大概率是先看下周围的人用什么，然后你就买什么，从众本质上也是一种相似（大众的选择就是方向），近朱者赤近墨者黑嘛。如果你说很独立自主，自己想买啥买啥，那也是对的，毕竟这玩意怎么搞都搞不到 100%。

关于多笔画（可跳过）

我们本文学的是单笔画，现在你可以稍微想下，如果是多笔画应该怎么搞？这里还是可以短暂的思考几秒种🤔。。。

举个具象点的例子，比如十这个字（这里仅仅是例子哈，不完全是这样）：

提取每个汉字的笔画特征，一般可以采集起始点、终点和中间的转折点。数据大概长下面这个样子：

采用上述的方式如果我写了个丁字是不是好像也能识别出来，大体都是一横一竖，有没有什么办法可以避免呢？当然是有的，现在我们每一笔保存的不再是点的坐标，而是该点与前一个点连线的角度，如果是每一笔的起始点，就拿上一笔的终点作为前一个点，说起来比较抽象，所以我又画了张图👇🏻（很简单的一张图，不要被吓到😂）：

大家想想如果是十字，在上图的第二个角度（绿2）中是不是就可以明显区分开了。另外我们只保存了两两点之间的角度，还省了不少空间呢。

看起来好像没问题了？不，还是差得远呢。你想想要是笔画顺序不对咋整。还是以十为例，我先写竖再写横咋整。啊这。。。其实还有其他识别方法，比如把文字按坐标轴切分成四块，分四段校验，这就不深入了，点到即止（毕竟就懂点皮毛）。

小结

以上就是手势识别的大致思路，虽然看起来是挺高大上的一个东西，但是读完之后应该觉得。不。。算难吧。。。有些东西不是你不会只是你不知道也没去尝试下，嘿嘿。最后，再次送上项目地址传送门，顺便附上我 canvas 专栏的另外两篇实战文章：

html2canvas 用着有问题？手写一个就知道为啥了💥

🔥用 canvas 来画个函数曲线吧！纵享丝滑

更多关于JS前端canvas手势识别的资料请关注脚本之家其它相关文章！

您可能感兴趣的文章:
阅读全文