首页 > 脚本专栏 > python > Python数据结构树

Python数据结构树与算法分析

2022-07-18 14:31:33 作者：Ding Jiaxiong

这篇文章主要介绍了Python数据结构树与算法分析，文章围绕主题展开详细的内容介绍，具有一定的参考价值，需要的小伙伴可以参考一下

1.示例

树的一些属性：

层次性：树是按层级构建的，越笼统就越靠近顶部，越具体则越靠近底部。
一个节点的所有子节点都与另一个节点的所有子节点无关。
叶子节点都是独一无二的。
嵌套

2.术语及定义

节点：树的基础部分。节点的名字 → 键，附加信息 → 有效载荷。
边：两个节点通过一条边相连，表示它们之间存在关系。除了根节点，其他每个结点都仅有一条入边，出边则可能有多条。
根节点：树中唯一没有入边的结点。
路径：由边连接的有序节点列表。
子节点：一个节点通过出边与子节点相连。
父节点：一个节点是其所有子节点的父节点。
兄弟节点：具有同一父节点的结点 → 互称兄弟节点。
子树：一个父节点及其所有后代的节点和边构成一棵子树。
叶子结点：叶子节点没有子节点。
层数：节点n的层数是从根节点到n的唯一路径长度。根节点的层数为0。
高度：树的高度是其中节点层数的最大值。

1.定义一：树由节点及连接节点的边构成。

树的属性：

有一个根节点除根节点外，其他每个节点都与其唯一的父节点相连。
从根节点到其他每个节点有且仅有一条路径。
如果每个节点最多有两个子节点 → 二叉树。

2.定义二：一棵树要么为空，要么由一个根节点和零棵或多棵子树构成，子树本身也是一棵树。

每棵子树的根节点通过一条边连到父树的根节点。

3.实现

3.1 列表之列表

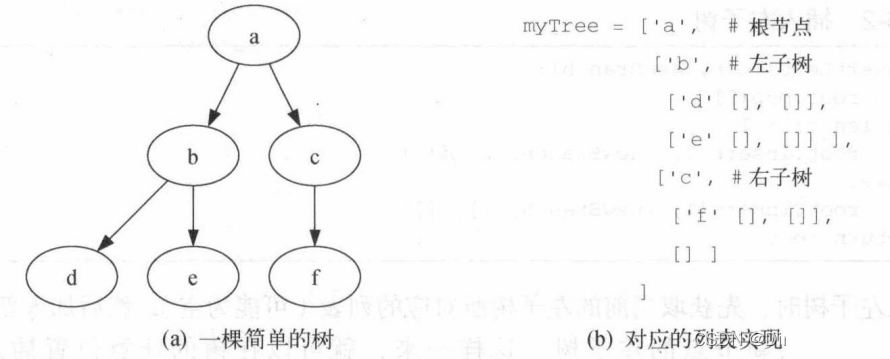
在这里插入图片描述

树的根节点是myTree[0]，左子树是myTree[1]，右子树是myTree[2]。

# 列表函数
def BinaryTree(r):
    return [r,[],[]] # 根节点r，和两个作为子节点的空列表
# 插入左子树
def insertLeft(root,newBranch):
    t = root.pop(1)
    if len(t) > 1:
        root.insert(1,[newBranch,t,[]])
    else:
        root.insert(1,[newBranch,[],[]])
    return root

## 插入右子树
def insertRight(root , newBranch):
    t = root.pop(2)
    if len(t) > 1:
        root.insert(2,[newBranch,[],t])
    else:
        root.insert(2,[newBranch,[],[]])
    return root
### 树的访问函数
def getRootVal(root):
    return root[0]
def setRootVal(root,newVal):
    root[0] = newVal
def getLeftChild(root):
    return root[1]
def getRightChild(root):
    return root[2]
r = BinaryTree(3)
insertLeft(r,4)
print(r)

3.2节点与引用

定义一个类，其中有根节点和左右子树的属性。

class BinaryTree:
    def __init__(self,rootObj):
        self.key = rootObj
        self.leftChild = None
        self.rightChild = None

    ## 插入左子节点
    def insertLeft(self,newNode):
        if self.leftChild == None:
            self.leftChild = BinaryTree(newNode)
        else:
            t = BinaryTree(newNode)
            t.left = self.leftChild
            self.leftChild = t
    ## 插入右子节点
    def insertRight(self,newNode):
        if self.rightChild == None:
            self.rightChild = BinaryTree(newNode)
        else:
            t = BinaryTree(newNode)
            t.right = self.rightChild
            self.rightChild = t
    ## 访问函数
    def getRightChild(self):
        return self.rightChild

    def getLeftChild(self):
        return self.leftChild

    def setRootVal(self,obj):
        self.key = obj
    def getRootVal(self):
        return self.key

4.二叉树的应用

4.1解析树

根据完全括号表达式构建解析树
如何计算解析树中的表达式
如何将解析树还原成最初的数学表达式

解析树构建器：

import operator

from pythonds.basic import Stack
from pythonds.trees import BinaryTree
def buildParseTree(fpexp):
    fplist = fpexp.split()
    pStack = Stack()
    eTree = BinaryTree("")
    pStack.push(eTree)
    currentTree = eTree

    for i in fplist:
        if i == "(":
            currentTree.insertLeft("")
            pStack.push(currentTree)
            currentTree = currentTree.getLeftChild()

        elif i not in "+-*/)":
            currentTree.setRootVal(eval(i))
            parent = pStack.pop()
            currentTree = parent
        elif i in "+-*/":
            currentTree.setRootVal(i)
            currentTree.insertRight("")
            currentTree = currentTree.getRightChild()
        elif i == ")":
            currentTree = pStack.pop()
        else:
            raise ValueError("Unkown Operator :" + i )
    return eTree

## 计算二叉解析树的递归函数
def evaluate(parseTree):
    opers = {
        "+":operator.add,"-":operator.sub,
        "*":operator.mul,"/":operator.truediv
    }
    
    leftC = parseTree.getLeftChild()
    rightC = parseTree.getRightChild()
    
    if leftC and rightC:
        fn = opers[parseTree.getRootVal()]
        return fn(evaluate(leftC),evaluate(rightC))
    else:
        return parseTree.getRootVal()

4.2树的遍历

前序遍历【根左右】
中序遍历【左根右】
后序遍历【左右根】

前序遍历算法实现为外部函数：

def preorder(tree):
    if tree:
        print(tree.getRootVal())
        preorder(tree.getLeftChild())
        preorder(tree.getRightChild)

前序遍历算法实现为BinaryTree类的方法

def preorder(self):
    print(self.key)
    if self.leftChild:
        self.leftChild.preorder()
    if self.rightChild:
        self.rightChild.preorder()

后序遍历函数

def postorder(tree):
    if tree != None:
        postorder(tree.getLeftChild())
        postorder(tree.getRightChild())
        print(tree.getRootVal())

中序遍历函数

def inorder(tree):
    if tree != None:
        inorder(tree.getLeftChild())
        print(tree.getRootVal())
        inorder(tree.getRightChild())

5.利用二叉堆实现优先级队列

队列一个重要的变体 → 优先级队列。和队列一样，优先级队列从头部移除元素，不过元素的逻辑顺序是由优先级决定的，优先级最高的元素在最前，最低的元素在最后。

实现优先级队列的经典方法 → 二叉堆。入队和出队操作均可达到O(logn)

最小堆【最小的元素一直在队首】
最大堆【最大的元素一直在队首】 6.6.2 二叉堆的实现

结构属性：

完全二叉树：除了最底层，其他每一层的节点都是满的。且在最底层，从左往右填充节点。
完全二叉树可以用一个列表直接表示。

堆的有序性：对于堆中任意元素x及其父元素p，p都不大于x。

堆操作

代码实现：

class EchaDui:
    # 新建二叉堆
    def __init__(self):
        self.heapList = [0]
        self.currentSize = 0
    
    def percUp(self,i):
        while i // 2 > 0:
            if self.heapList[i] < self.heapList[i // 2]:
                tmp = self.heapList[i // 2]
                self.heapList[i // 2] = self.heapList[i]
                self.heapList[i] = tmp
                
            i = i // 2
    # 新加元素
    def insert(self,k):
        self.heapList.append(k)
        self.currentSize = self.currentSize + 1
        self.percUp(self.currentSize)
        
    def percDown(self,i):
        while (i * 2) <= self.currentSize:
            mc = self.minChild(i)
            if self.heapList[i] > self.heapList[mc]:
                tmp = self.heapList[i]
                self.heapList[i] = self.heapList[mc]
                self.heapList[mc] = tmp
            i = mc
    def minChild(self,i):
        if i * 2 + 1 > self.currentSize:
            return i * 2
        else:
            if self.heapList[i*2] < self.heapList[i*2 + 1]:
                return i * 2
            else:
                return i * 2 + 1
    ## 从二叉堆中删除最小的元素
    def delMin(self):
        retval = self.heapList[1]
        self.heapList[1] = self.heapList[self.currentSize]
        self.currentSize = self.currentSize - 1
        self.heapList.pop()
        self.percDown(1)
        return retval
        
    ## 根据元素列表构建堆
    def builgHeap(self,alist):
        i = len(alist) // 2
        self.currentSize = len(alist)
        self.heapList = [0] + alist[:]
        while (i > 0):
            self.percDown(i)
            i = i - 1

6.二叉搜索树

6.1搜索树的实现

二叉搜索树依赖性质：小于父节点的键都在左子树中，大于父节点的键则都在右子树。