解决BN和Dropout共同使用时会出现的问题
作者:sliderSun
BN与Dropout共同使用出现的问题
BN和Dropout单独使用都能减少过拟合并加速训练速度,但如果一起使用的话并不会产生1+1>2的效果,相反可能会得到比单独使用更差的效果。
相关的研究参考论文:Understanding the Disharmony between Dropout and Batch Normalization by Variance Shift
本论文作者发现理解 Dropout 与 BN 之间冲突的关键是网络状态切换过程中存在神经方差的(neural variance)不一致行为。
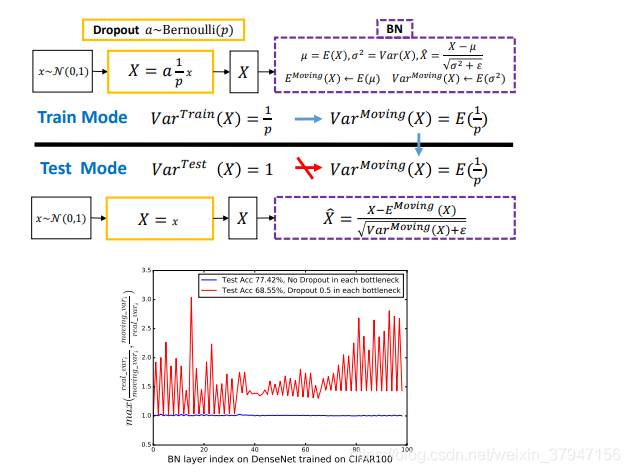
试想若有图一中的神经响应 X,当网络从训练转为测试时,Dropout 可以通过其随机失活保留率(即 p)来缩放响应,并在学习中改变神经元的方差,而 BN 仍然维持 X 的统计滑动方差。
这种方差不匹配可能导致数值不稳定(见下图中的红色曲线)。
而随着网络越来越深,最终预测的数值偏差可能会累计,从而降低系统的性能。
简单起见,作者们将这一现象命名为「方差偏移」。
事实上,如果没有 Dropout,那么实际前馈中的神经元方差将与 BN 所累计的滑动方差非常接近(见下图中的蓝色曲线),这也保证了其较高的测试准确率。

作者采用了两种策略来探索如何打破这种局限。
一个是在所有 BN 层后使用 Dropout,另一个就是修改 Dropout 的公式让它对方差并不那么敏感,就是高斯Dropout。
第一个方案比较简单
把Dropout放在所有BN层的后面就可以了,这样就不会产生方差偏移的问题,但实则有逃避问题的感觉。
第二个方案
来自Dropout原文里提到的一种高斯Dropout,是对Dropout形式的一种拓展。作者进一步拓展了高斯Dropout,提出了一个均匀分布Dropout,这样做带来了一个好处就是这个形式的Dropout(又称为“Uout”)对方差的偏移的敏感度降低了,总得来说就是整体方差偏地没有那么厉害了。
BN、dropout的几个问题和思考
1、BN的scale初始化
scale一般初始化为1.0。
联想到权重初始化时,使用relu激活函数时若采用随机正太分布初始化权重的公式是sqrt(2.0/Nin),其中Nin是输入节点数。即比一般的方法大了2的平方根(原因是relu之后一半的数据变成了0,所以应乘以根号2)。
那么relu前的BN,是否将scale初始化为根号2也会加速训练?
这里主要有个疑点:BN的其中一个目的是统一各层的方差,以适用一个统一的学习率。那么若同时存在sigmoid、relu等多种网络,以上方法会不会使得统一方差以适应不同学习率的效果打了折扣?
没来得及试验效果,如果有试过的朋友请告知下效果。
2、dropout后的标准差改变问题
实践发现droput之后改变了数据的标准差(令标准差变大,若数据均值非0时,甚至均值也会产生改变)。
如果同时又使用了BN归一化,由于BN在训练时保存了训练集的均值与标准差。dropout影响了所保存的均值与标准差的准确性(不能适应未来预测数据的需要),那么将影响网络的准确性。
若输入数据为正太分布,只需要在dropout后乘以sqrt(0.5)即可恢复原来的标准差。但是对于非0的均值改变、以及非正太分布的数据数据,又有什么好的办法解决呢?
3、稀疏自编码的稀疏系数
稀疏自编码使用一个接近0的额外惩罚因子来使得隐层大部分节点大多数时候是抑制的,本质上使隐层输出均值为负数(激活前),例如惩罚因子为0.05,对应sigmoid的输入为-3.5,即要求隐层激活前的输出中间值为-3.5,那么,是不是可以在激活前加一层BN,beta设为-3.5,这样学起来比较快?
经过测试,的确将BN的beta设为负数可加快训练速度。因为网络初始化时就是稀疏的。
但是是不是有什么副作用,没有理论上的研究。
4、max pooling是非线性的,avg pooling是线性的
总结
以上为个人经验,希望能给大家一个参考,也希望大家多多支持脚本之家。
