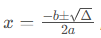利用Python实现二次方程求根的深度指南

在数学计算、工程建模、物理分析等场景中，二次方程ax²+bx+c=0（a≠0）的求根是基础且核心的需求。手动计算需反复处理判别式与求根公式，而 Python 可通过模块化代码实现自动化求解，兼顾效率与准确性。本文将对一段二次方程求根代码进行逐行解析，结合数学逻辑与编程规范，带大家理解其设计思路与实践价值。

一、代码功能与核心逻辑概述

给定代码通过 3 个核心函数实现二次方程求解：

• get_float_number()：确保用户输入合法浮点数，处理输入异常
• solve_quadratic_equation()：基于求根公式计算根（支持复数根）
• main()：串联程序流程，实现用户交互与结果输出

整体逻辑遵循 “输入验证→公式计算→结果展示” 的工程化思路，同时通过cmath模块解决了传统math模块无法处理负判别式的问题，确保所有二次方程（a≠0）都能得到有效解。

二、代码逐模块深度解析

1. 依赖模块导入：import cmath

代码首行导入cmath（复数数学模块），而非常用的math模块，核心原因是：

二次方程判别式Δ=b²−4ac 存在三种情况：

• Δ>0：两个不相等实根
• Δ=0：两个相等实根（重根）
• Δ<0：两个共轭复根

math.sqrt()仅支持非负实数输入，若Δ<0会抛出ValueError；而cmath.sqrt()可直接处理负数，返回复数形式的结果（如1+2j），确保求解完整性。

2. 输入验证函数：get_float_number(prompt)

该函数负责获取用户输入的合法浮点数，是程序 “鲁棒性” 的关键，需重点关注异常处理逻辑：

def get_float_number(prompt):
    """
    用于获取一个浮点数
    :param prompt:提示信息
    :return:用户输入的浮点数
    """
    while True:  # 无限循环，直到输入合法
        try:
            return float(input(prompt))  # 尝试将输入转为float，合法则返回
        except ValueError:  # 若输入无法转为float（如字母、符号），捕获异常
            print("输入错误，请重新输入")

设计亮点：

• try-except异常捕获：避免用户输入非数字（如 “abc”“12a”）导致程序崩溃，符合 “容错性设计” 原则；
• while True循环：强制用户反复输入，直到合法为止，确保后续计算的输入有效性；
• 参数化提示prompt：函数不固定提示文本，而是通过参数传入，提高复用性（可用于 a、b、c 三个系数的输入）。

3. 核心计算函数：solve_quadratic_equation(a, b, c)

该函数实现二次方程求根公式的代码转化，需结合数学逻辑理解：

def solve_quadratic_equation(a, b, c):
    """
    求解二次方程 ax^2 + bx + c = 0 的根
    :param a: 二次项系数（需满足a≠0）
    :param b: 一次项系数
    :param c: 常数
    :return: 两个根（实根或复根）
    """
    delta = (b ** 2 - 4 * a * c)  # 计算判别式Δ
    root1 = (-b + cmath.sqrt(delta)) / (2 * a)  # 求根公式1
    root2 = (-b - cmath.sqrt(delta)) / (2 * a)  # 求根公式2
    return root1, root2

数学严谨性说明：

• 前提条件：函数默认传入的a ≠ 0（后续main函数会验证此条件），否则方程退化为一次方程 bx+c=0，不属于二次方程范畴；
• 求根公式正确性：严格遵循数学公式​​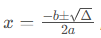，无计算逻辑偏差；
• 复数根处理：当Δ<0时，cmath.sqrt(delta)返回虚数（如根号−3=1.7320508075688772j），最终root1和root2为共轭复根（如−0.5+0.8660254037844386j与−0.5−0.8660254037844386j）。

4. 程序入口函数：main()

main函数是程序的 “控制中枢”，负责串联输入、计算、输出全流程，关键逻辑在于二次项系数a的额外验证：

def main():
    print("欢迎使用二次方程求根程序")
    # 1. 获取二次项系数a，确保a≠0
    a = get_float_number("请输入二次项系数 a：")
    while a == 0:  # 单独验证a≠0，避免非二次方程
        print("二次项系数不能为 0，请重新输入")
        a = get_float_number("请输入二次项系数 a：(a ≠ 0)")

    # 2. 获取一次项系数b和常数c（无特殊限制，可为0）
    b = get_float_number("请输入一次项系数 b：")
    c = get_float_number("请输入常数 c：")

    # 3. 计算并输出结果
    root1, root2 = solve_quadratic_equation(a, b, c)
    print("方程的根为：{0} 和 {1}".format(root1, root2))

流程设计细节：

• a的双重验证：先通过get_float_number()确保a是浮点数，再通过while a == 0强制a≠0，避免 “伪二次方程” 计算；
• 用户体验优化：提示文本清晰（如(a ≠ 0)补充说明），结果输出用format格式化，可读性强；
• 职责分离：不将计算逻辑直接写在main中，而是调用solve_quadratic_equation()，符合 “模块化设计” 原则，便于后续维护。

三、实际运行案例演示

为验证代码有效性，我们针对判别式的三种情况设计测试用例，实际运行结果如下：

案例 1：Δ > 0（两个不相等实根）

输入：

欢迎使用二次方程求根程序
请输入二次项系数 a：1
请输入一次项系数 b：-5
请输入常数 c：6

输出：

方程的根为：(3+0j) 和 (2+0j)

说明：根为实根 3 和 2，cmath自动将实根表示为虚部为 0 的复数（3+0j），不影响实际使用。

案例 2：Δ = 0（重根）

输入：

欢迎使用二次方程求根程序
请输入二次项系数 a：1
请输入一次项系数 b：2
请输入常数 c：1

输出：

方程的根为：(-1+0j) 和 (-1+0j)

说明：两个根完全相等，符合重根的数学定义。

案例 3：Δ < 0（共轭复根）

输入：

欢迎使用二次方程求根程序
请输入二次项系数 a：1
请输入一次项系数 b：1
请输入常数 c：1

输出：

方程的根为：(-0.5+0.8660254037844386j) 和 (-0.5-0.8660254037844386j)

说明：根为共轭复数，虚部绝对值相等、符号相反，计算结果正确。

四、代码优势分析

鲁棒性强：通过try-except处理输入异常，a≠0验证避免逻辑错误，可应对多种非法输入；

功能完整：支持所有二次方程（包括复根），无求解盲区；

可维护性高：函数分工明确（输入验证、计算、控制流程分离），代码结构清晰，便于后续修改；

用户友好：提示文本简洁明确，结果输出格式化，降低使用门槛。

五、进阶改进方向

尽管代码已实现核心功能，但仍可从 “实用性”“扩展性” 角度优化：

1. 根类型智能判断与友好输出

当前输出统一为复数形式（如3+0j），可添加判别式判断，对实根、重根、复根分别输出更易懂的格式：

def judge_root_type(delta):
    if delta > 1e-9:  # 考虑浮点误差，不用delta>0
        return "两个不相等实根"
    elif abs(delta) < 1e-9:
        return "两个相等实根（重根）"
    else:
        return "两个共轭复根"

# 在solve_quadratic_equation中添加类型返回
def solve_quadratic_equation(a, b, c):
    delta = b**2 - 4*a*c
    root_type = judge_root_type(delta)
    root1 = (-b + cmath.sqrt(delta))/(2*a)
    root2 = (-b - cmath.sqrt(delta))/(2*a)
    # 实根去掉虚部（如3+0j→3.0）
    if "实根" in root_type:
        root1 = root1.real
        root2 = root2.real
    return root1, root2, root_type

# 输出时补充类型说明
print(f"方程的根类型：{root_type}，根为：{root1} 和 {root2}")

2. 支持多次求解

当前程序运行一次只能求解一个方程，可添加循环支持多次计算：

def main():
    print("欢迎使用二次方程求根程序")
    while True:
        # 原有输入、计算逻辑...
        print(f"方程的根为：{root1} 和 {root2}")
        # 询问是否继续
        again = input("是否继续求解下一个方程？(y/n)：").lower()
        if again != "y":
            print("程序结束，再见！")
            break

3. 浮点误差优化

由于计算机浮点计算精度限制，当 Δ 接近 0 时（如delta = 1e-16），可能误判为 “不相等实根”，需通过极小值（如1e-9）判断：

# 替代原delta > 0的判断
if delta > 1e-9:  # 大于极小值，视为Δ>0
    return "两个不相等实根"
elif abs(delta) < 1e-9:  # 绝对值小于极小值，视为Δ=0
    return "重根"

六、总结与学习启示

这段二次方程求根代码虽短，却涵盖了 Python 核心知识点：

• 函数设计：模块化分工、参数传递、返回值处理；
• 异常处理：try-except捕获输入错误，提升程序稳定性；
• 数学应用：将求根公式转化为代码，兼顾实根与复根；
• 用户交互：清晰的提示与输出，优化使用体验。

对于 Python 初学者，它是 “数学 + 编程” 结合的典型案例；对于工程开发者，其鲁棒性设计与模块化思路也值得借鉴。通过理解代码逻辑、尝试改进优化，不仅能掌握二次方程求解的实现方法，更能培养 “工程化编程思维”—— 让代码既正确，又易用、易维护。

以上就是利用Python实现二次方程求根的深度指南的详细内容，更多关于Python二次方程求根的资料请关注脚本之家其它相关文章！