关于pytorch求导总结(torch.autograd)

1、Autograd 求导机制

我们在用神经网络求解PDE时， 经常要用到输出值对输入变量（不是Weights和Biases）求导；

例如在训练WGAN-GP 时， 也会用到网络对输入变量的求导，pytorch中通过 Autograd 方法进行求导

其求导规则如下：

1.1当x为向量，y为一标量时

通过autograd 计算的梯度为：

1.2先假设x,y为一维向量

其对应的jacobi(雅可比）矩阵为

grad_outputs 是一个与因变量 y 的shape 一致的向量

在给定grad_outputs 后，通过Autograd 方法 计算的梯度如下:

1.3当 x 为1维向量，Y为2维向量

给出grad_outputs与Y的shape一致

Y 与x的jacobi矩阵

则 Y 对 x 的梯度:

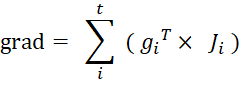
1.4当 X ，Y均为2维向量时

​​​​​​​

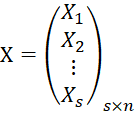
1.5当XY为更高维度时

可以按照上述办法转化为低维度的求导

值得注意的是：

求导后的梯度shape总与自变量X保持一致对自变量求导的顺序并不会影响结果，某自变量的梯度值会放到该自变量原来相同位置梯度是由每个自变量的导数值组成的向量，既有大小又有方向grad_outputs 与 因变量Y的shape一致，每一个参数相当于对因变量中相同位置的y进行一个加权。

2、pytorch求导方法

2.1在求导前需要对需要求导的自变量进行声明

2.2torch.autograd.gard()

grad =  autograd.grad( outputs, inputs, grad_outputs=None, retain_graph=None,    create_graph=False, only_inputs=True, allow_unused=False )

参数解释：

• outputs:求导的因变量 Y
• inputs : 求导自变量 X
• grad_outputs:

当outputs为标量时，grad_outputs=None , 不需要写，当outputs 为向量，需要为其声明一个与outputs相同shape的参数矩阵，该矩阵中的每个参数的作用是，对outputs中相同位置的y进行一个加权。

不然会报错

autograd.grad()返回的是元组数据类型，元组的长度与inputs长度相同，元组中每个单位的shape与相同位置的inputs相同

retain_graph:

1、当求完一次梯度后默认会把图信息释放掉，都会free掉计算图中所有缓存的buffers，当要连续进行几次求导时，可能会因为前面buffers不存在而报错。

因为第二个梯度计算z对x的导数，需要y对x的计算导数的缓存信息，但是在计算grad1后，保存信息被释放，找不到了，因此报错。

修改如下：

2、一般计算的最后一个梯度可以不需要保存计算图信息，这样在计算后可以及时释放掉占用的内存。

3、在pytorch中连续多次调用backward()也会出现这样的问题,对中间的backwad()，需要保持计算图信息

create_graph: 若要计算高阶导数，则必须选为True

求二阶导方法如下：

allow_unused: 允许输入变量不进入计算

2.3torch.backward()

def backward(
                        gradient: Optional[Tensor] = None,
                        retain_graph: Any = None,
                        create_graph: Any = False,
                        inputs: Any = None) -> Any
                                                )

如果需要计算导数，可以在tensor上直接调用.backward(),会返回该tensor所有自变量的导数。

通过name(自变量名).grad 可以获得该自变量的梯度如果tensor是标量，则backward()不需要指定任何参数如果tensor是向量，则backward()需要指定gradient一个与tensorshape相同的参数矩阵，即这里的gradient 同 grad_outputs 作用和形式完全一样。

总结

以上为个人经验，希望能给大家一个参考，也希望大家多多支持脚本之家。