C++并查集的原理与使用方法
作者:落羽的落羽
并查集是一种树型的数据结构,用于处理不相交集合的合并及查询问题,下面这篇文章主要介绍了C++并查集原理与使用方法的相关资料,文中通过代码介绍的非常详细,需要的朋友可以参考下
一、并查集的概念
在一些场景中,需要将n个不同元素划分为一些不相交的集合。开始时,每个元素各成一个元素,然后按一定的规律将属于同一组的元素合并。这个过程中需要反复用到查询一个元素是否属于某个集合的算法。适合用于这种场景的数据结构是并查集(Union-Find Set)!
并查集的底层结构本质上是一片森林(多棵树的集合)
比如,我现在有九个数据元素,给他们编号0~8:

按照某种需求,这些数据被分组合并为:
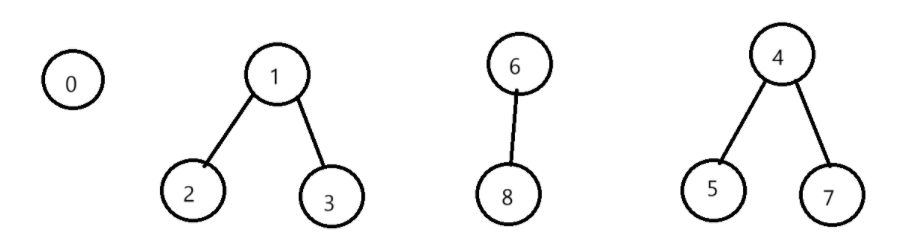
按照其他需求,这些树可以继续合并下去…
而这个森林,可以用一个数组记录下来元素的关系!
我们可以规定并查集用数组下标代表每个元素,数组内容代表元素之间的关系:
- 数组下标代表元素编号
- 如果数组内容为负整数,代表这个下标是根,绝对值表示它这棵树的元素个数
- 如果数组内容为非负整数,代表这个下标不是根,数组内容是它的父亲在数组中的下标
比如,上面的森林例子,用并查集数组表示,就是:
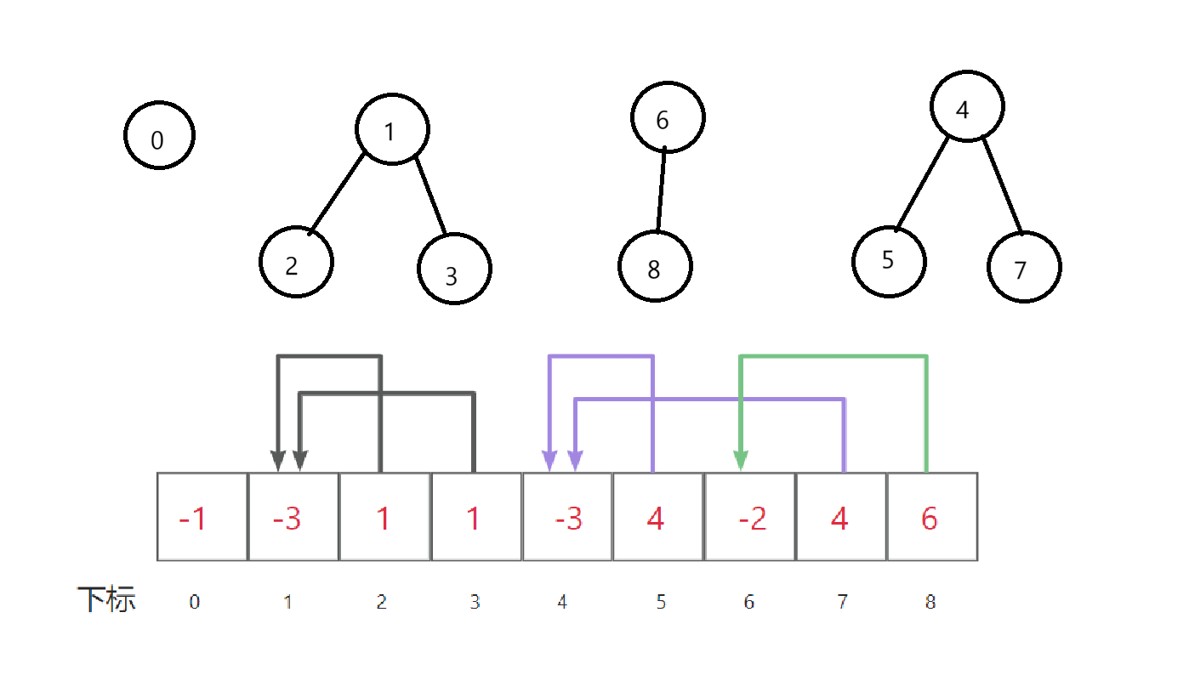
如果元素的数据类型不能直接作为数组下标,只要在实现中用std::map之类的结构,建立元素到下标的映射关系,就能解决了!
通过并查集的特点,可以看出并查集一般能解决:
- 查找元素属于哪个集合:沿着数组一直找到元素为负数,就是根
- 查看两个元素是否属于一个集合:看看这两个元素的根是否相同
- 将两个集合归并为一个集合:假如要将下标a的树合并到下标b的树中,arr[b] += arr[a],arr[a] = b即可,即令1成为0的一个孩子
- 统计集合的个数:统计数组中元素为负数的个数
二、并查集的实现
#pragma once
#include<vector>
#include<iostream>
using namespace std;
class UnionFindSet
{
public:
UnionFindSet(int size)
:_set(size, -1) // 初始时每个数据各是一棵树,元素均为-1
{ }
// 查找一个数据属于哪个集合,找根元素的下标
int FindRoot(int i)
{
while (_set[i] >= 0)
{
i = _set[i];
}
return i;
}
// 合并两个数据所在的集合
void Union(int i1, int i2)
{
// 找这两个数据的根下标
int root1 = FindRoot(i1);
int root2 = FindRoot(i2);
if (root1 != root2)
{
_set[root1] += _set[root2];
_set[root2] = root1;
}
// 如果root1 == root2,说明这两个数据本就在一个集合,不用合并
}
// 判断两个数据是否在同一个集合
bool IsSameSet(int i1, int i2)
{
return FindRoot(i1) == FindRoot(i2);
}
// 统计集合个数
int SetCount()
{
int ret = 0;
for (int n : _set)
{
if (n < 0)
ret++;
}
return ret;
}
private:
vector<int> _set;
};
测试:
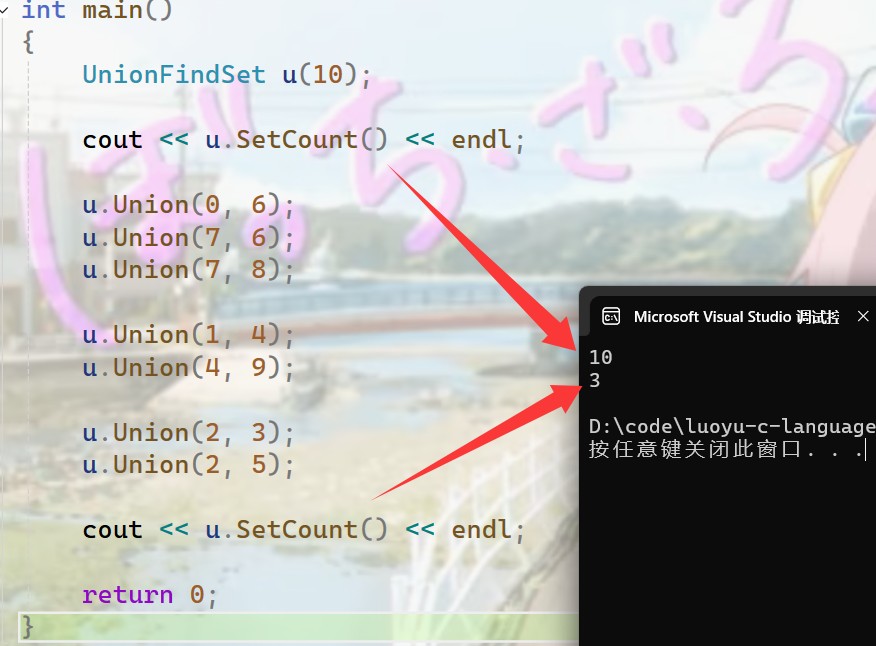
三、算法题中的应用
并查集的特点在某些算法题中很有用:
class Solution {
public:
// 并查集, 统计集合数量
int findCircleNum(vector<vector<int>>& isConnected) {
vector<int> ufs(isConnected.size(), -1);
auto findRoot = [&ufs](int i)
{
while(ufs[i] >= 0)
{
i = ufs[i];
}
return i;
};
auto Union = [&ufs, &findRoot](int i1, int i2)
{
int root1 = findRoot(i1);
int root2 = findRoot(i2);
if(root1 != root2)
{
ufs[root1] += ufs[root2];
ufs[root2] = root1;
}
};
auto SetCount = [&ufs]()
{
int ret = 0;
for(int n : ufs)
{
if(n < 0)
ret++;
}
return ret;
};
for(int i = 0; i < isConnected.size(); i++)
{
for(int j = 0; j < isConnected[i].size(); j++)
{
if(isConnected[i][j] == 1)
{
Union(i, j);
}
}
}
return SetCount();
}
};
class Solution {
public:
// 并查集,数组大小26
// 遍历一次把所有==的两个字母放到一个集合,再遍历一次看!=的两个字符是否都在集合中出现过,出现过则false
bool equationsPossible(vector<string>& equations) {
vector<int> ufs(26, -1);
auto findRoot = [&ufs](int i)
{
while(ufs[i] >= 0)
{
i = ufs[i];
}
return i;
};
auto Union = [&ufs, &findRoot](int i1, int i2)
{
int root1 = findRoot(i1);
int root2 = findRoot(i2);
if(root1 != root2)
{
ufs[root1] += ufs[root2];
ufs[root2] = root1;
}
};
for(string& s : equations)
{
if(s[1] == '=')
{
Union(s[0]-'a', s[3]-'a');
}
}
for(string& s : equations)
{
if(s[1] == '!')
{
int root1 = findRoot(s[0]-'a');
int root2 = findRoot(s[3]-'a');
if(root1 == root2)
{
return false;
}
}
}
return true;
}
};
总结
到此这篇关于C++并查集的原理与使用方法的文章就介绍到这了,更多相关C++并查集原理与使用内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家!


