C++双指针的实践

2025-11-11 11:02:56 作者：MzKyle

双指针算法通过设置两个指针遍历数据结构,有效优化时间和空间复杂度,适用于链表操作、数组处理和字符串匹配等场景,本文就来详细的介绍一下C++双指针,具有一定的参考价值,感兴趣的可以了解一下

在C++编程中，双指针算法是一种高效的解题思路，其核心是通过设置两个指针（或索引）遍历数据结构（如数组、链表、字符串等），利用指针的移动规则减少无效操作，从而将时间复杂度从暴力解法的O(n²)优化至O(n)或O(n log n)。这种算法广泛应用于链表操作、数组处理、字符串匹配等场景。

一、双指针算法的核心思想

双指针算法的本质是通过两个指针的协同移动，缩小问题的处理范围。与暴力解法中嵌套循环的“盲目遍历”不同，双指针的移动具有明确的逻辑（如基于数据的有序性、结构特性等），从而避免冗余计算。

其核心优势体现在：

时间优化：将多层循环转化为单层遍历，降低时间复杂度；
空间优化：多数情况下无需额外空间（原地操作），空间复杂度可保持O(1)；
逻辑清晰：通过指针的移动规则直观反映问题的解决思路。

二、双指针的常见类型及应用场景

根据指针的移动方向和作用，双指针可分为三大类：快慢指针、左右指针、同向指针。以下结合具体场景详细讲解。

（一）快慢指针（Floyd’s Tortoise and Hare）

快慢指针指两个指针以不同速度遍历数据结构（如链表中，快指针每次走2步，慢指针每次走1步）。其核心应用是处理链表中的环问题和查找特定位置（如中间节点）。

1. 链表环检测（LeetCode 141）

问题：判断一个单链表是否存在环。
暴力解法：用哈希表记录访问过的节点，若重复访问则有环，时间O(n)但空间O(n)。
双指针解法：

设快指针fast和慢指针slow，初始均指向头节点；
fast每次移动2步，slow每次移动1步；
若链表有环，fast会先进入环并绕环移动，最终与slow在环内相遇；
若fast到达nullptr，则无环。

代码实现：

struct ListNode {
    int val;
    ListNode *next;
    ListNode(int x) : val(x), next(nullptr) {}
};

bool hasCycle(ListNode *head) {
    if (head == nullptr || head->next == nullptr) return false;
    ListNode *slow = head;
    ListNode *fast = head->next; // 初始错开，避免直接相遇
    while (slow != fast) {
        if (fast == nullptr || fast->next == nullptr) return false;
        slow = slow->next;       // 慢指针走1步
        fast = fast->next->next; // 快指针走2步
    }
    return true;
}

时间复杂度：O(n)（无环时fast走n/2步；有环时相遇前slow最多走n步）。
空间复杂度：O(1)（仅用两个指针）。

2. 寻找环的入口（LeetCode 142）

问题：若链表有环，找到环的入口节点。
算法思路：

先用快慢指针判断有环，记录相遇点meet；
让slow从头节点出发，fast从meet出发，两者均每次走1步；
两指针再次相遇的节点即为环的入口。

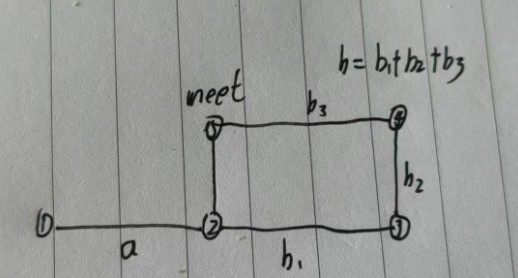
原理：设头节点到入口距离为a，入口到相遇点距离为b，环长为c。则相遇时：

slow走了a + b；
fast走了a + b + k*c（绕环k圈）；
因fast速度是slow的2倍，故2*(a + b) = a + b + k*c → a = k*c - b b=k*c-a。
因此，slow从头部走a步，与fast从meet走k*c - b步（等价于绕环k圈后回到入口）相遇。

重置slow = 0,fast仍在meet处（等价于初始走了a+b），当slow=a(slow走了a步)，fast=a+b+kc-b=a+kc，所以a,b在环的入口相遇

代码实现：

ListNode *detectCycle(ListNode *head) {
    if (head == nullptr) return nullptr;
    ListNode *slow = head, *fast = head;
    // 第一步：找到相遇点
    do {
        if (fast->next == nullptr || fast->next->next == nullptr) return nullptr;
        slow = slow->next;
        fast = fast->next->next;
    } while (slow != fast);
    // 第二步：寻找入口
    slow = head;
    while (slow != fast) {
        slow = slow->next;
        fast = fast->next;
    }
    return fast;
}

3. 寻找链表的中间节点（LeetCode 876）

问题：返回单链表的中间节点（若长度为偶数，返回第二个中间节点）。
算法思路：

快指针每次走2步，慢指针每次走1步；
当fast到达尾节点时，slow恰好指向中间节点。

代码实现：

ListNode* middleNode(ListNode* head) {
    ListNode *slow = head, *fast = head;
    while (fast != nullptr && fast->next != nullptr) {
        slow = slow->next;
        fast = fast->next->next;
    }
    return slow;
}

（二）左右指针（相向指针）

左右指针指两个指针分别从数据结构的两端出发，相向而行（左指针从左向右，右指针从右向左），多用于有序数组/字符串的处理。其核心是利用数据的有序性，通过指针移动排除无效解。

1. 两数之和（有序数组版，LeetCode 167）

问题：给定有序数组nums和目标值target，找到两个数使得和为target，返回索引（下标从1开始）。
暴力解法：嵌套循环遍历所有组合，时间O(n²)。
双指针解法：

左指针left初始指向0，右指针right指向n-1；
计算当前和sum = nums[left] + nums[right]：
- 若sum == target，返回[left+1, right+1]；
- 若sum > target，说明右指针太大，right--；
- 若sum < target，说明左指针太小，left++。

原理：数组有序保证了指针移动的有效性——当sum > target时，减小右指针可降低总和；当sum < target时，增大左指针可提高总和，无需检查其他组合。

代码实现：

vector<int> twoSum(vector<int>& nums, int target) {
    int left = 0, right = nums.size() - 1;
    while (left < right) {
        int sum = nums[left] + nums[right];
        if (sum == target) {
            return {left + 1, right + 1};
        } else if (sum > target) {
            right--;
        } else {
            left++;
        }
    }
    return {-1, -1}; // 题目保证有解，此行为冗余
}

时间复杂度：O(n)，空间复杂度O(1)。

2. 反转字符串（LeetCode 344）

问题：原地反转字符串（如["h","e","l","l","o"]→["o","l","l","e","h"]）。
算法思路：

左指针left指向0，右指针right指向n-1；
交换nums[left]与nums[right]，然后left++、right--，直到left >= right。

代码实现：

void reverseString(vector<char>& s) {
    int left = 0, right = s.size() - 1;
    while (left < right) {
        swap(s[left], s[right]);
        left++;
        right--;
    }
}

3. 二分查找（本质是左右指针的变体）

二分查找中，left和right指针分别指向搜索范围的两端，通过比较中间值与目标值，不断缩小范围，本质是左右指针的“跳跃式移动”。

代码实现：

int search(vector<int>& nums, int target) {
    int left = 0, right = nums.size() - 1;
    while (left <= right) {
        int mid = left + (right - left) / 2; // 避免溢出
        if (nums[mid] == target) return mid;
        else if (nums[mid] < target) left = mid + 1;
        else right = mid - 1;
    }
    return -1;
}

（三）同向指针（一前一后指针）

同向指针指两个指针从同一端出发，沿相同方向移动（通常一个在前“探索”，一个在后“记录”），多用于数组去重、子数组/子串问题。

1. 删除有序数组中的重复项（LeetCode 26）

问题：原地删除有序数组中的重复元素，返回新长度（如[1,1,2]→长度2，数组变为[1,2]）。
算法思路：

慢指针slow记录有效元素的尾位置（初始0）；
快指针fast遍历数组（初始1）；
若nums[fast] != nums[slow]，说明找到新元素，slow++并将nums[fast]复制到nums[slow]；
最终slow + 1为新长度。

代码实现：

int removeDuplicates(vector<int>& nums) {
    if (nums.empty()) return 0;
    int slow = 0;
    for (int fast = 1; fast < nums.size(); fast++) {
        if (nums[fast] != nums[slow]) {
            slow++;
            nums[slow] = nums[fast];
        }
    }
    return slow + 1;
}

2. 移动零（LeetCode 283）

问题：将数组中的0移到末尾，保持非零元素的相对顺序（如[0,1,0,3,12]→[1,3,12,0,0]）。
算法思路：

慢指针slow记录非零元素的尾位置（初始0）；
快指针fast遍历数组，若nums[fast] != 0，则交换nums[slow]与nums[fast]，slow++；
遍历结束后，slow及之后的位置全部赋0。

代码实现：

void moveZeroes(vector<int>& nums) {
    int slow = 0;
    for (int fast = 0; fast < nums.size(); fast++) {
        if (nums[fast] != 0) {
            swap(nums[slow], nums[fast]);
            slow++;
        }
    }
    // 剩余位置补0（可选，因原数组0已被交换到后面）
    for (int i = slow; i < nums.size(); i++) {
        nums[i] = 0;
    }
}

3. 滑动窗口（同向指针的高级应用）

滑动窗口是同向指针的典型场景，用于解决子数组/子串的最值问题（如最长、最短、包含特定元素等）。其核心是用left和right指针维护一个“窗口”，通过移动right扩张窗口，移动left收缩窗口，在O(n)时间内找到最优解。

示例：长度最小的子数组（LeetCode 209）
问题：给定数组nums和目标值s，找到和≥s的最短子数组长度（若无则返回0）。

算法思路：

left和right初始均为0，sum记录窗口内元素和；
移动right，将nums[right]加入sum；
当sum ≥ s时，尝试移动left缩小窗口，更新最小长度；
重复直至right遍历结束。

代码实现：

int minSubArrayLen(int s, vector<int>& nums) {
    int n = nums.size();
    int min_len = INT_MAX;
    int left = 0, sum = 0;
    for (int right = 0; right < n; right++) {
        sum += nums[right];
        // 收缩窗口
        while (sum >= s) {
            min_len = min(min_len, right - left + 1);
            sum -= nums[left];
            left++;
        }
    }
    return min_len == INT_MAX ? 0 : min_len;
}

时间复杂度：O(n)（每个元素被right和left各访问一次）。

三、双指针算法的进阶技巧

指针初始化的灵活性：
快慢指针初始可不同步（如环检测中fast比slow超前一步）；左右指针可从非端点出发（如处理子数组时限制窗口范围）。
结合数据结构特性：
有序数组优先考虑左右指针；链表问题优先考虑快慢指针；子串问题优先考虑滑动窗口（同向指针）。
多指针扩展：
某些场景需3个指针（如荷兰国旗问题：用left、mid、right划分0、1、2），核心思想与双指针一致。
边界条件处理：
需注意指针越界（如链表fast->next是否为nullptr）、空数据结构（如数组长度为0）等特殊情况。

双指针算法是C++编程中优化效率的核心思想之一，其核心在于通过指针的协同移动减少无效遍历。根据应用场景可分为快慢指针（链表环、中间节点）、左右指针（有序数组、反转）、同向指针（去重、滑动窗口）三大类，每种类型均通过明确的移动规则将时间复杂度从O(n²)降至O(n)。

到此这篇关于C++双指针的实践的文章就介绍到这了,更多相关C++双指针内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家！

您可能感兴趣的文章:

C++如何将二叉搜索树转换成双向循环链表(双指针或数组)