Java算法之计数排序、桶排序、基数排序实现代码
作者:Brookty
这篇文章主要介绍了Java算法之计数排序、桶排序、基数排序实现的相关资料,分别通过计数、分桶和位数处理实现高效稳定排序,文中通过代码及图文介绍的非常详细,需要的朋友可以参考下
鸽巢原理
鸽子归巢,待排序数据归到有序组群中按大小归进有序组群来排,数越大,归到的有序组就在越后的,数越小,归到的有序组就在越前的
- 如果有序组以一个元素一个元素划分的,实现的是元素组归巢排序,即计数排序
- 如果有序组按范围多个元素为一组划分的,实现的是范围组归巢排序,即桶排序
一、计数排序
1.实现
1.1步骤
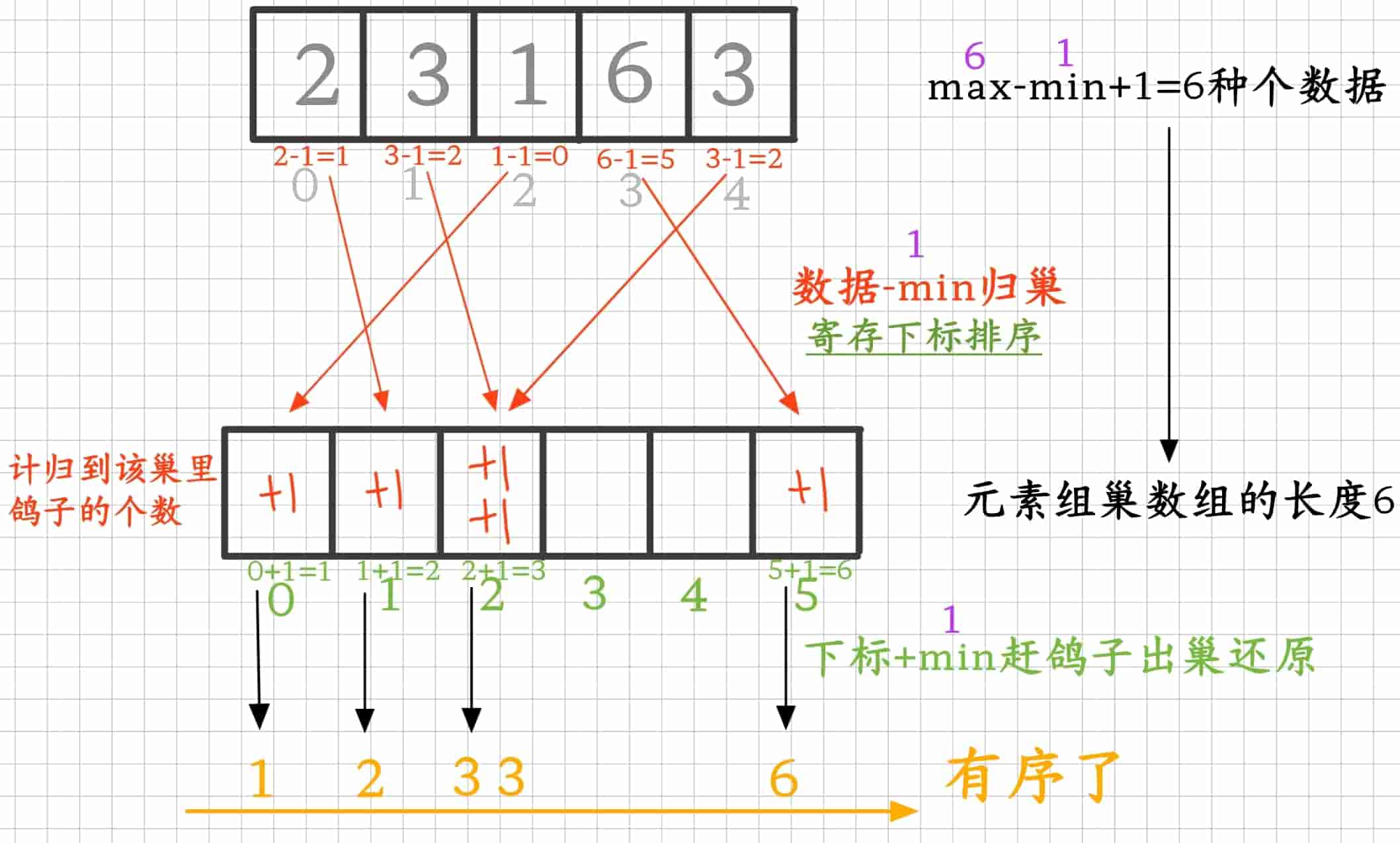
- 开辟数据范围内的所有元素都有各自对应的元素组巢穴,范围内一共有多少种个数据,就开辟每种个数据都有对应的多大的数组,比如90(max) - 10(min) = 80(种个数据)
- 归巢时,通过该数据-数据范围内的最小值得到所归巢的下标,然后在数组元素巢中计数表示归巢
- 因为巢内只有一种个数据直接就是有序的,所以所有数据归完巢在巢层面有序时所有数据就已经有序了,最后将它们按顺序地赶出巢加回去即得原来有序的数据
1.2代码
public static void countSort(int[] array) {
//1.求当前数据的最大值和最小值
int minVal = array[0];
int maxVal = array[0];
for (int i = 1; i < array.length; i++) {
if(array[i] < minVal) {
minVal = array[i];
}
if(array[i] > maxVal) {
maxVal = array[i];
}
}
//2.根据数据最大值和最小值来确定元素组巢穴数组的大小
int[] count = new int[maxVal-minVal+1];
//3.遍历原来的数据进行归巢排序
for (int i = 0; i < array.length; i++) {
count[array[i]-minVal]++;
}
//4.将元素组巢穴里已排好序的数据按顺序写回array
int index = 0;//重新表示array数组的下标
for (int i = 0; i < count.length; i++) {
while (count[i] > 0) {
array[index] = i+minVal;
index++;
count[i]--;
}
}
}
}
2.性质
2.1稳定性
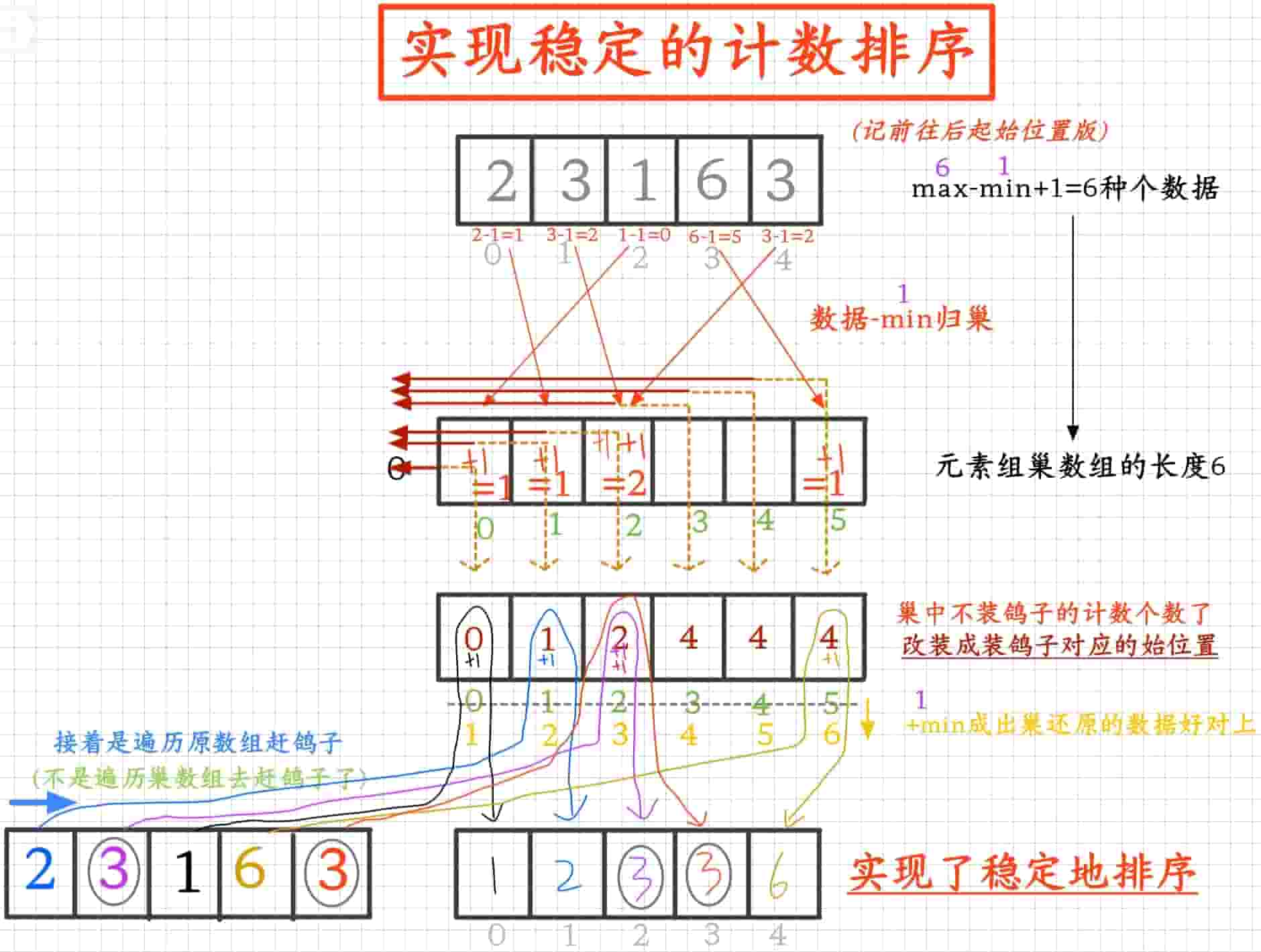
将每个数据都归到巢中完成有序时,根据巢中有序来的元素的计数个数,可以将巢改装成装每种个元素有序排的始位置,通过对应顺序遍历原数组将数据正确稳定地放在排好序的各自位置上,能实现稳定的排序,所以计数排序是稳定的排序
2.1.1从前往后前始版:
原本巢中装的是鸽子的计数数量,现在巢里面改装成装种个鸽子从前往后的起始位置来进行排序:
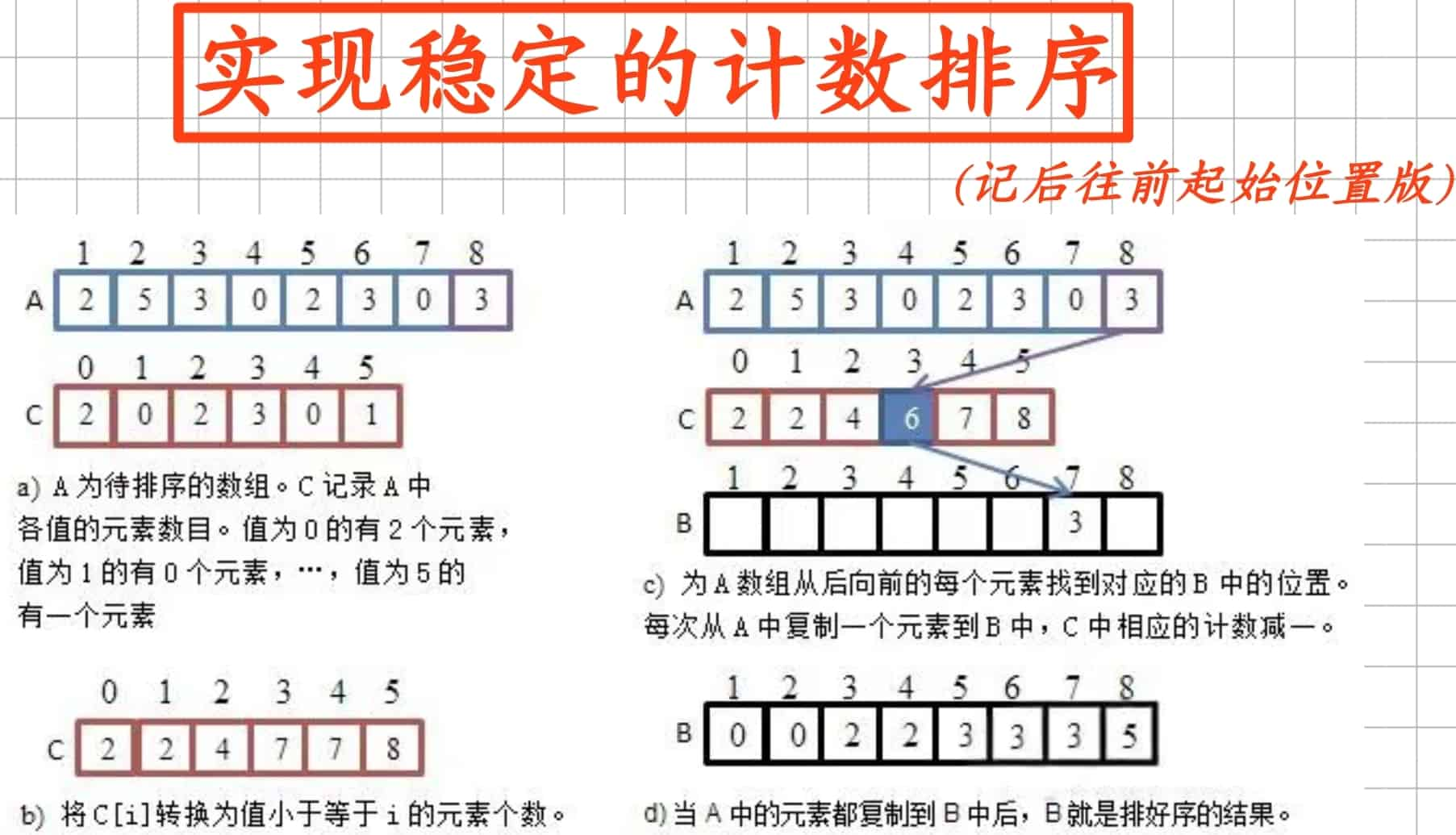
2.1.2从后往前末始版:
巢里面改装成装种个鸽子从后往前的起始位置来进行排序:
2.2复杂度
2.2.1时间复杂度
找最大最小值确定范围种个数据遍历原数组用了n,原数组数据每个去归巢用了n,范围x种个元素巢每个去赶,所以时间复杂度为2n + x,即O(n+x)
2.2.2空间复杂度
范围x种个数据需要开辟x个元素巢的数组,所以空间复杂度为O(x)
二、桶排序
1.实现
1.1步骤
- 开辟数据范围内所有元素都有对应的范围数组组巢穴,将所有数据入范围组巢穴先进行第一轮巢穴外的排好序,此时巢外已经有序了
- 再进行第二轮各自巢穴内的排好序,此时就巢外、巢内都有序所有数据都有序了
- 最后按顺序地将它们从数组巢中赶出即得有序的数据

1.2代码
public static int[] bucketSort(int[] arr) {
// 边界条件:空数组或单个元素直接返回
if (arr.length <= 1) {
return arr.clone();
}
// Step 1: 确定数据范围
int minVal = Integer.MAX_VALUE;
int maxVal = Integer.MIN_VALUE;
for (int num : arr) {
if (num < minVal) minVal = num;
if (num > maxVal) maxVal = num;
}
// 处理所有元素相同的情况
if (maxVal == minVal) {
return arr.clone();
}
// Step 2: 初始化桶
int bucketCount = (int) Math.sqrt(arr.length) + 1; // 桶数量=数组长度的平方根(经验值)
double bucketRange = (double)(maxVal - minVal) / bucketCount;
List<List<Integer>> buckets = new ArrayList<>(bucketCount);
for (int i = 0; i < bucketCount; i++) {
buckets.add(new ArrayList<>());
}
// Step 3: 元素分配到桶中
for (int num : arr) {
// 计算元素应该属于哪个桶
int index = (int)((num - minVal) / bucketRange);
// 处理最大值刚好落在最后一个桶外的情况
if (index == bucketCount) index--;
buckets.get(index).add(num);
}
// Step 4: 对每个桶内部排序
for (List<Integer> bucket : buckets) {
Collections.sort(bucket); // 使用内置排序算法,决定了桶排序的稳定性
}
// Step 5: 合并桶
int[] sortedArr = new int[arr.length];
int idx = 0;
for (List<Integer> bucket : buckets) {
for (int num : bucket) {
sortedArr[idx++] = num;
}
}
return sortedArr;
}2.稳定性
稳定性取决于在第二轮巢内开始排相同大小的元素时所用的排序方法是否具有稳定性
三、基数排序
1.原理
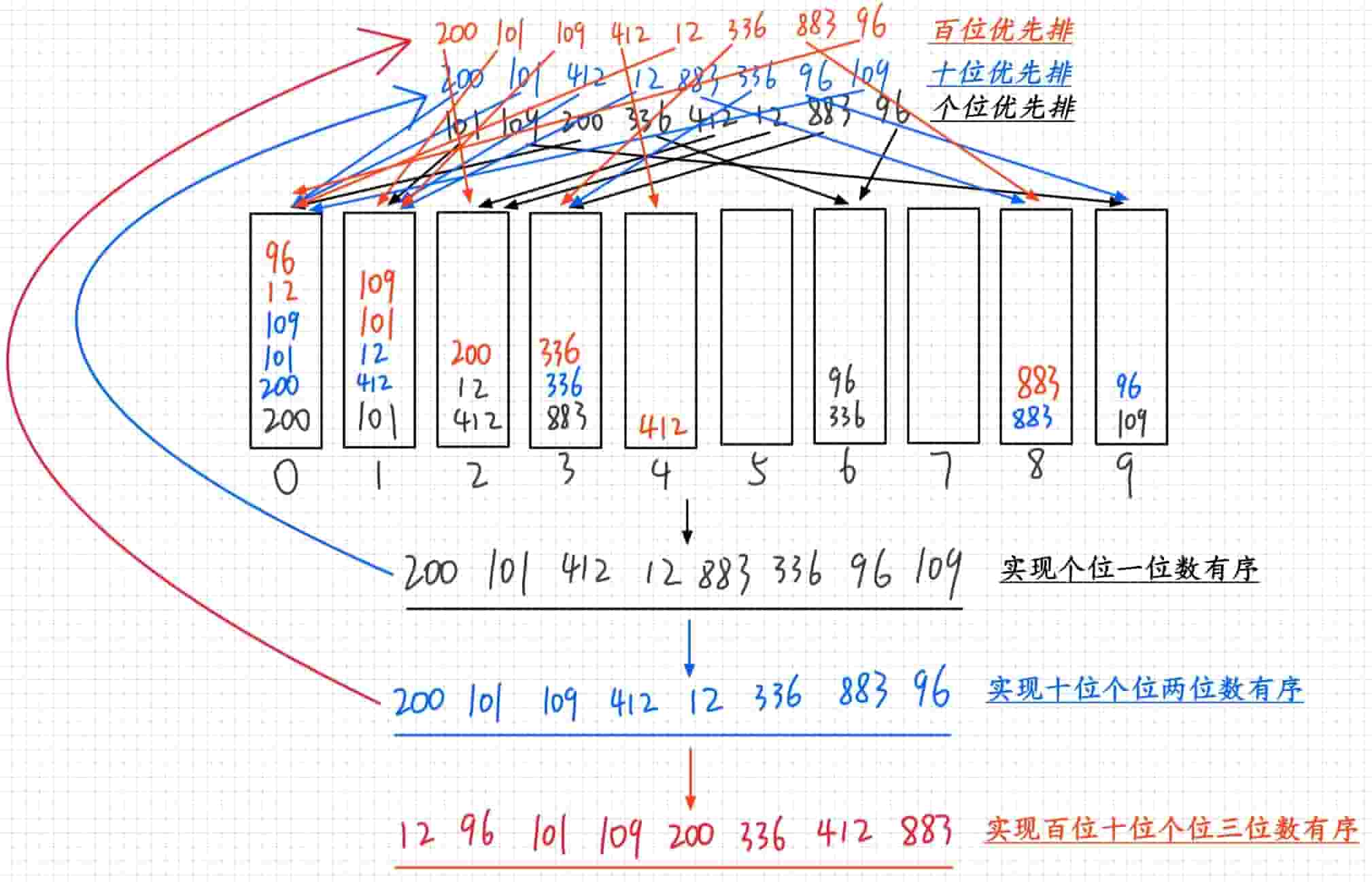
- 先进行个位排序,能实现个位一位数有序
- 个位有序下,再进行十位优先排序,能实现十位个位两位数有序
- 十个位有序下,再进行百位优先排序,能实现百位十位个位三位数有序
2.代码
public static int[] radixSort(int[] arr) {
if (arr.length <= 1) {
return arr.clone();
}
// Step 1: 确定最大数的位数
int maxNum = Integer.MIN_VALUE;
for (int num : arr) {
if (num > maxNum) maxNum = num;
}
// Step 2: 按每位进行计数排序(从低位到高位)
int exp = 1; // 从个位开始
while (maxNum / exp > 0) {
// 初始化10个数字桶(0-9)
List<List<Integer>> buckets = new ArrayList<>(10);
for (int i = 0; i < 10; i++) {
buckets.add(new ArrayList<>());
}
// 按当前位分配到桶中
for (int num : arr) {
int digit = (num / exp) % 10; // 提取当前位的数字
buckets.get(digit).add(num);
}
// 重组数组
int idx = 0;
for (List<Integer> bucket : buckets) {
for (int num : bucket) {
arr[idx++] = num;
}
}
exp *= 10; // 处理更高位
}
return arr;
}总结
到此这篇关于Java算法之计数排序、桶排序、基数排序实现的文章就介绍到这了,更多相关java计数排序、桶排序、基数排序内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家!
