Java算法之归并排序举例详解

一、归并排序的递归探寻

1.思路

理想结果等于成分解断开子结果表达式的公式表示

快速排序：

整个数组有序 = 其中一个元素有序 + 其左断开数组有序 + 其右断开数组有序

归并排序：

整个数组有序 = 左断开数组有序 + 右断开数组有序 + 两有序数组的有序合并

2.搭建

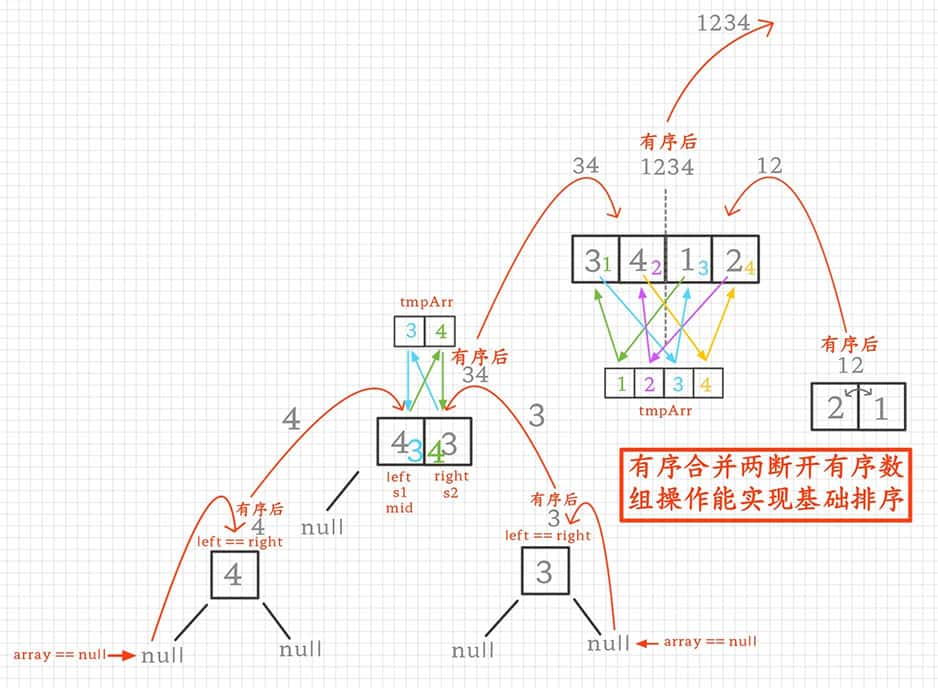
2.1设计过掉不符情况（在最底层时）

• if(array == null) return， 数组没有元素不用排，下面是有元素
• if(left == right) return，只有一个元素已经是有序了不用排，下面是多个元素
• if(left > right) return，排不了不要排的，之后下面是符合一般情况的多个元素 

2.2查验能实现基础排序（在最底层往上点时）

在最底层往上点时，有序数组有序合并操作在最底层能实现两元素之间的比较然后进行排序的

2.3跳转结果继续往上回搭：

跳转有序数组结果继续往上有序合并维护回搭

3.实质

从底层的最小单个断开有序数组往上有序地合并成越来越大的断开有序数组直至合并完成一个整体的有序数组

4.实现

    public static void mergeSort(int[] array) {
        mergeSortFunc(array,0,array.length-1);
    }

    private static void mergeSortFunc(int[] array,int left,int right) {
        if(left >= right) return;
        int mid = (left+right) / 2;

        mergeSortFunc(array,left,mid);
        mergeSortFunc(array,mid+1,right);
        merge(array,left,right,mid);
    }

    private static void merge(int[] array, int left, int right, int mid) {
        int s1 = left;
        int s2 = mid+1;
        int[] tmpArr = new int[right-left+1];
        int k = 0;
        //证明两个区间 都同时有数据的
        while (s1 <= mid && s2 <= right) {
            if(array[s2] <= array[s1]) {
                tmpArr[k++] = array[s2++];
            }else {
                tmpArr[k++] = array[s1++];
            }
        }
        while (s1 <= mid) {
            tmpArr[k++] = array[s1++];
        }
        while (s2 <= right) {
            tmpArr[k++] = array[s2++];
        }
        //tmpArr 里面一定是这个区间内有序的数据了
        for (int i = 0; i < tmpArr.length; i++) {
            array[i+left] = tmpArr[i];
        }
    }

二、递归的调用栈

1.递归的执行过程

在函数递归中，调用的函数里面执行着再调用着随着形参深入的不断变化的函数自己：

第一次调用函数的执行转去等着第二次调用函数的执行完，第二次调用函数的执行也卡着转去等第三次调用函数的执行完，一层层形参变化着重复地执行调用而都没有往下去return，直到最后调用函数传的形参变化到符合return的条件不再继续往下调用了，return出结果开始往回地一层层促进上一层没有执行完到执行完return，即开始往回地执行往回地归

2.递归的函数栈帧

所有任意一个函数的调用都会独立开辟新的函数栈帧(里面存放局部变量、函数形参、返回地址、寄存器值）压入调用栈中，在函数执行到return语句结束后才弹出栈：

递归调用时，函数栈帧从先往后地一个个独立地压入栈中，往下递归直到形参条件变到return后由最新函数调用的栈帧开始往上弹栈帧出调用栈，在开始往上弹出栈帧开始有执行完往回层往下执行时，方法里面有可能写的是继续又去执行调用当前层形参条件下的再来一波函数递归调用(形参变化可能就去设置成不同的了就会是左右不一样的分支)，即是二叉即二叉树的情况：

• 每一层不仅要左边往下全执行到底层然后开始往上全执行到它那层的左边结束，接着又要执行右边的往下执行到底层然后再往上全执行完到它的右层结束，最后它这个节点对应的这层函数才也执行完它的栈帧也弹出调用栈，二叉树从大到小所有的结构都是左边往下全执行完往上回来、右边往下全执行完往上回来、接着它这个节点的栈帧也往上弹返回执行完 

2.1递归函数的栈帧压弹

在归并排序的二叉树递归调用过程中：

• 每次累计着往下调用到底层时，此时的调用栈所占的空间是最大的、深度在二叉树的最底层，调用栈的空间计算为调用栈里栈帧的个数×每个栈帧的内存大小，在每个函数的栈帧中，函数里面那些函数的调用信息、并非循环出现的常量个数的局部变量空间和都可算成常数的大小，所以在归并排序这里，调用栈的最大空间为在调用栈里栈帧个数最多的时候：树的高度log(n)*每个函数栈帧的内存大小是常数，即log(n)*常数，函数调用执行完最底层后就开始有往上返回了，往上弹出最新最顶的栈帧
• 然后执行完返回到上层时又回到当前层条件下的且新的形参变化模式的再往下递归，又会去压栈到最底层，此时调用栈的空间又达到最大的log(n)
• 当它右边往下的也全执行完又往上返回到当前层时，就开始继续往下接着执行就开始有去调用合并有序数组的函数了

2.2合并有序数组函数的栈帧压弹

执行调用合并有序数列的函数时，调用栈又会压入合并有序数组函数的栈帧，里面存放有开辟的当前层数组元素个数大小的数组(非常量级的，要算的)，此时总的占用空间为调用栈的空间log(n-...)+n(-...)，因为合并有序数组函数的栈帧每次都是处在栈顶压入的且函数里面并没有再调用函数的在它之上再压栈，所以它每次在栈顶进来压栈完就紧接着弹出栈的

三、归并排序的复杂度

1.空间复杂度

空间复杂度计算的是整个执行所有时刻中出现的最大瞬时占用空间：

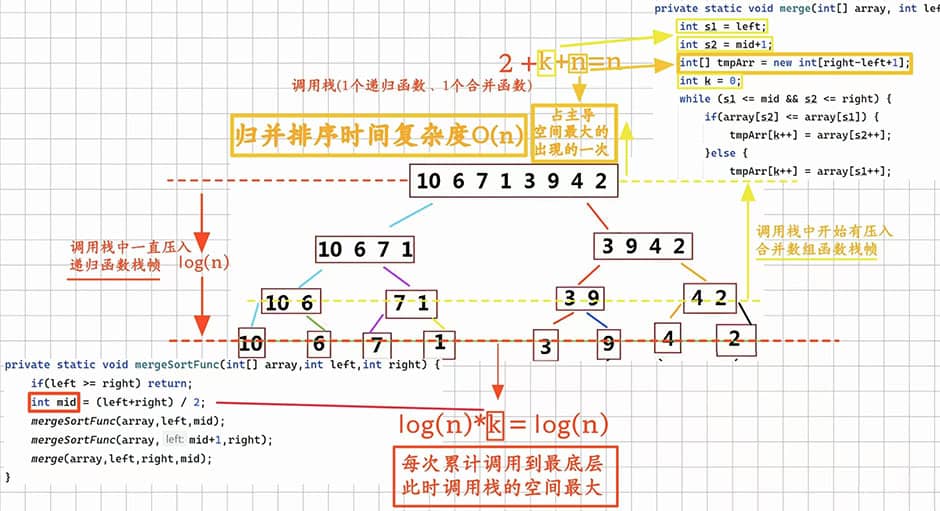
从下层往上层的返回的过程中，递归函数的调用栈空间变小着、合并有序数组的函数栈帧在变大着(里面的数组越来越大的)：

• 在最底层时占用的空间为递归函数的调用栈空间log(n)+合并有序数组的函数栈帧0，即log(n)+0=log(n)
• 当到达最上层第一层时，递归函数的调用栈空间是1，而合并有序数组的函数栈帧空间是n，此时的总空间大小是n，相比于最底层的log(n)及从下往上的过程中log(n)的递减、n的递增的总空间，此时的n是整个执行所有时刻中出现的最大瞬时占用的空间，所以归并排序的空间复杂度是O(n)

2.时间复杂度

时间复杂度即算整个递归调用执行过程的时间和，我们可以不用按着递归搜索的过程去时时累计总的算，直接站在总二叉树的角度一层一层地算所有时间的和就行了，一层层里面每一个树节点及下的全执行完对应着该调用函数的全执行完，因为递归调用语句mergeSortFunc(array,left,mid)都是且已转成里面的函数节点内容来算了(调用中的去执行调用部分是常量级的已不算)，且if(left >= right) return、int mid = (left+right) / 2也都是常量级的执行时间不算，对应到总的时间就是计算所有函数节点里的merge(array,left,right,mid)合并有序数组的时间和，每一层所有函数节点的合并有序数组时间和都为n(除了最后一层的函数节点进去就直接判断为return没执行有序数组合并)，一共有log(n)层，所以时间复杂度为O(n*log(n)) 

总结

到此这篇关于Java算法之归并排序的文章就介绍到这了,更多相关Java算法归并排序内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家！