C#实现三元组的使用示例
作者:神仙别闹
本文介绍了C#中的三元组数据结构,以及如何使用三元组在C#中进行一些特定的计算,具有一定的参考价值,感兴趣的可以了解一下
我们知道矩阵是一个非常强大的数据结构,在动态规划以及各种图论算法上都有广泛的应用,当然矩阵有着不足的地方就是空间和时间复杂度都维持在 N2 上,比如 1w 个数字建立一个矩阵,在内存中会占用 1w*1w=1 亿的类型空间,这时就会遇到 outofmemory。。。那么面临的一个问题就是如何来压缩矩阵,当然压缩的方式有很多种,这里就介绍一个顺序表的压缩方式:三元组。
一、三元组
有时候我们的矩阵中只有零星的一些非零元素,其余的都是零元素,那么我们称之为稀疏矩阵,当然没有绝对的说有多少个零元素才算稀疏。
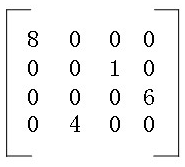
针对上面的这个无规律的存放非零元素,三元组提出了一种方法,就是仅仅记录矩阵中的非零元素以及它的行,列以及值 N(x,y,v)构成的一个三元组,标识一个稀疏矩阵的话,还要记录该矩阵的阶数,这样我们就将一个二维的变成了一个一维,极大的压缩的存储空间,这里要注意的就是,三元组的构建采用“行“是从上到下,“列”也是从左到右的方式构建的顺序表。

/// <summary>
/// 三元组
/// </summary>
public class Unit
{
public int x;
public int y;
public int element;
}
/// <summary>
/// 标识矩阵
/// </summary>
public class SPNode
{
//矩阵总行数
public int rows;
//矩阵总列数
public int cols;
//非零元素的个数
public int count;
//矩阵中非零元素
public List<Unit> nodes = new List<Unit>();
}
其实说到这里也就差不多了,我们只要知道三元组是用来做矩阵压缩的一个顺序存储方式即可,然后知道怎么用三元组表来做一些常规的矩阵运算,好了,既然说已经做成线性存储了,那就做个“行列置换”玩玩。
二、行列置换
做行列置换很容易,也就是交换"非零元素"的(x,y)坐标,要注意的就是,原先我们的三元组采用的是”行优先“,所以在做转置的时候需要遵循"列优先“。

/// <summary>
/// 行转列运算
/// </summary>
/// <param name="spNode"></param>
/// <returns></returns>
public SPNode ConvertSpNode(SPNode spNode)
{
//矩阵元素的x和y坐标进行交换
SPNode spNodeLast = new SPNode();
//行列互换
spNodeLast.rows = spNode.cols;
spNodeLast.cols = spNode.rows;
spNodeLast.count = spNode.count;
//循环原矩阵的列数 (行列转换)
for (int col = 0; col < spNode.cols; col++)
{
//循环三元组行的个数
for (int sp = 0; sp < spNode.count; sp++)
{
var single = spNode.nodes[sp];
//找到三元组中存在的相同编号
if (col == single.y)
{
spNodeLast.nodes.Add(new Unit()
{
x = single.y,
y = single.x,
element = single.element
});
}
}
}
return spNodeLast;
}
最后是总的代码:
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Diagnostics;
using System.Threading;
using System.IO;
namespace ConsoleApplication2
{
public class Program
{
public static void Main()
{
Martix martix = new Martix();
//构建三元组
var node = martix.Build();
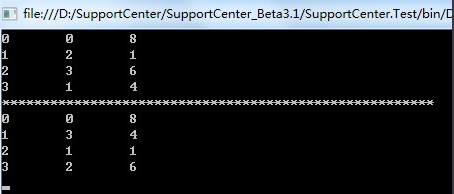
foreach (var item in node.nodes)
{
Console.WriteLine(item.x + "\t" + item.y + "\t" + item.element);
}
Console.WriteLine("******************************************************");
var mynode = martix.ConvertSpNode(node);
foreach (var item in mynode.nodes)
{
Console.WriteLine(item.x + "\t" + item.y + "\t" + item.element);
}
Console.Read();
}
}
public class Martix
{
/// <summary>
/// 三元组
/// </summary>
public class Unit
{
public int x;
public int y;
public int element;
}
/// <summary>
/// 标识矩阵
/// </summary>
public class SPNode
{
//矩阵总行数
public int rows;
//矩阵总列数
public int cols;
//非零元素的个数
public int count;
//矩阵中非零元素
public List<Unit> nodes = new List<Unit>();
}
/// <summary>
/// 构建一个三元组
/// </summary>
/// <returns></returns>
public SPNode Build()
{
SPNode spNode = new SPNode();
//遵循行优先的原则
spNode.nodes.Add(new Unit() { x = 0, y = 0, element = 8 });
spNode.nodes.Add(new Unit() { x = 1, y = 2, element = 1 });
spNode.nodes.Add(new Unit() { x = 2, y = 3, element = 6 });
spNode.nodes.Add(new Unit() { x = 3, y = 1, element = 4 });
//4阶矩阵
spNode.rows = spNode.cols = 4;
//非零元素的个数
spNode.count = spNode.nodes.Count;
return spNode;
}
/// <summary>
/// 行转列运算
/// </summary>
/// <param name="spNode"></param>
/// <returns></returns>
public SPNode ConvertSpNode(SPNode spNode)
{
//矩阵元素的x和y坐标进行交换
SPNode spNodeLast = new SPNode();
//行列互换
spNodeLast.rows = spNode.cols;
spNodeLast.cols = spNode.rows;
spNodeLast.count = spNode.count;
//循环原矩阵的列数 (行列转换)
for (int col = 0; col < spNode.cols; col++)
{
//循环三元组行的个数
for (int sp = 0; sp < spNode.count; sp++)
{
var single = spNode.nodes[sp];
//找到三元组中存在的相同编号
if (col == single.y)
{
spNodeLast.nodes.Add(new Unit()
{
x = single.y,
y = single.x,
element = single.element
});
}
}
}
return spNodeLast;
}
}
}
到此这篇关于C#实现三元组的使用示例的文章就介绍到这了,更多相关C# 三元组内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家!
