Scala排序算法之归并排序解析
作者:哇哈哈水有点甜
这篇文章主要介绍了Java排序算法之归并排序解析,简介:归并排序是一种经典的排序算法,它采用分治的思想,将待排序的数组不断地分割成小的子数组,然后再将这些子数组合并成有序的数组,需要的朋友可以参考下
Scala实现归并排序解析
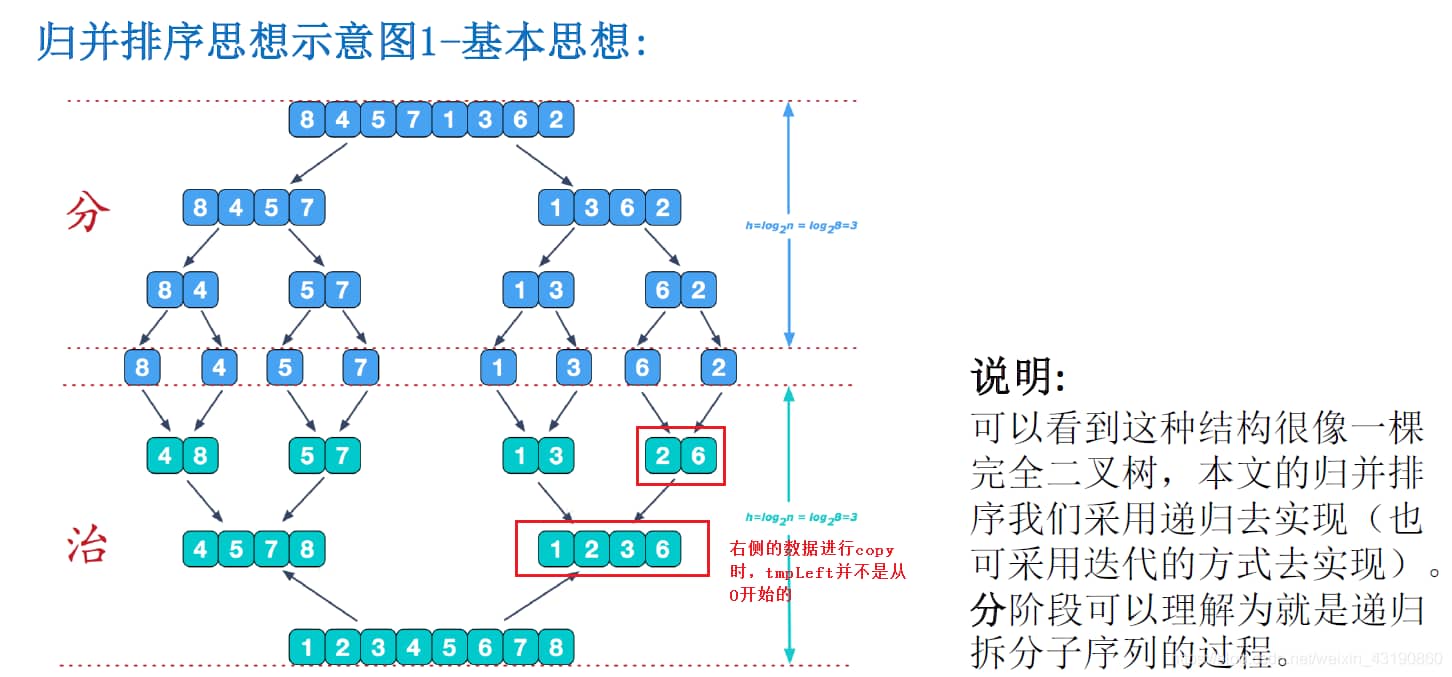
利用归并的思想实现的排序方法,该算法采用经典的分治(divide-and-conquer)策略(分治法将问题分(divide)成一些小的问题,然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案“修补”在一起,即分而治之)
优势:
对于巨大的数据集,如果要求Top N这种操作,由于不能把数据一次性读进内存,快排无法发挥作用,这时可以采取归并的方法,将大的数据集分成多个小的数据集,然后分别求Top N,再进行归并,最后从归并的结果中求出Top N。
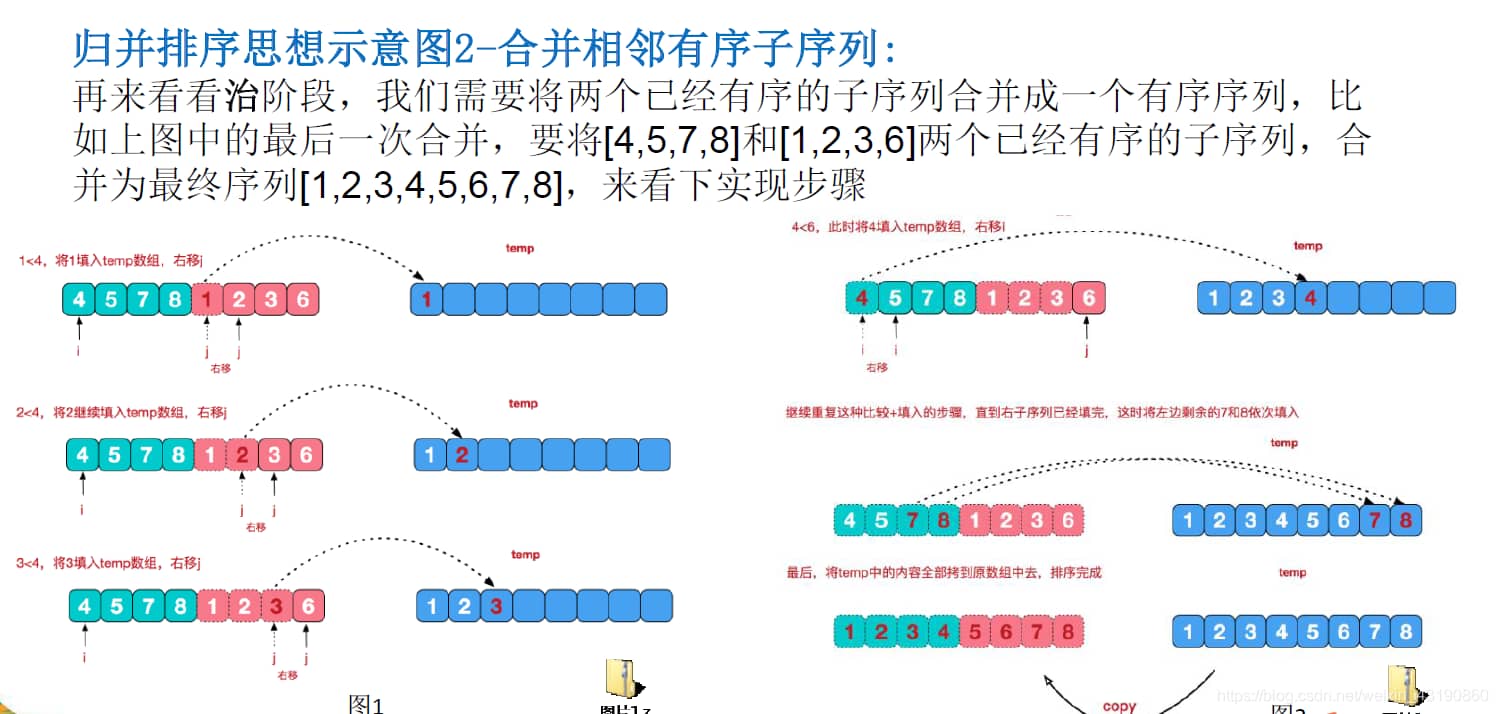
代码实现(Scala)
object MergeSort {
/**
* 测试归并排序
* @param args
*/
def main(args: Array[String]): Unit = {
var arr = Array(-8, 4, 1, 889, 56, -37)
var tmp = new Array[Int](arr.length)
mergeSort(arr, 0, arr.length-1, tmp)
for (elem <- arr) {
println(elem)
}
}
/**
*
* @param arr 待排序的数组
* @param left :最初的左边的下标:0
* @param right :最初的右边下标:length-1
* @param tmp :临时数组,事先开辟好的,大小和arr一样
*/
def mergeSort(arr: Array[Int], left: Int, right: Int, tmp: Array[Int]): Unit = {
if (left < right) {
//只要left<right,就可以继续分,直到将所有元素全部打散成单个
//取数组中间值下标
val mid = (left + right) / 2
//对数组中间元素左侧递归切分
mergeSort(arr, left, mid, tmp)
//对数组中间元素右侧递归切分
mergeSort(arr, mid + 1, right, tmp)
//merge是合并的操作
merge(arr, left, mid, right, tmp)
}
}
def merge(arr: Array[Int], left: Int, mid: Int, right: Int, tmp: Array[Int]) = {
var i = left //左边的开始下标
var j = mid + 1 //右边的开始下标
var t = 0 //临时数组tmp的下标
while (i <= mid && j <= right) {//同时满足这两个条件,说明中间元素左右两侧均还有元素未放到临时排序数组中
if (arr(i) <= arr(j)) {
//如果当前的左边的有序列表的值小于当前的右边有序列表的值,把小的值拷贝到tmp数组中,然后下标后移1位
tmp(t) = arr(i)
i += 1
t += 1
} else {
tmp(t) = arr(j)
t += 1
j += 1
}
}
//不满足第一个while条件说明有一侧数据已经全部拷贝到tmp数组中了
while (i <= mid) {
//如果左边的有序列表中还有数据,依次拷贝到tmp数组中
tmp(t) = arr(i)
i += 1
t += 1
}
while (j <= right) {
//如果右边的有序列表中还有数据,依次拷贝到tmp数组中
tmp(t) = arr(j)
j += 1
t += 1
}
//将本次的tmp数组的数据拷贝到原数组arr中
t = 0
//注意这里原数组下标tmpLeft不从0开始,而是从left开始,因为
var tmpLeft = left
while (tmpLeft <= right) {
arr(tmpLeft) = tmp(t)
tmpLeft += 1
t += 1
}
}
}
到此这篇关于Scala排序算法之归并排序解析的文章就介绍到这了,更多相关Scala实现归并排序解析内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家!
