java

关注公众号 jb51net

关闭
首页 > 软件编程 > java > Java跳表

跳表的由来及Java实现详解

作者：日拱一車

跳表（Skip List）是一种基于链表的数据结构，它可以支持快速的查找、插入、删除操作，本文主要来和大家讲讲跳表的由来与实现，感兴趣的小伙伴可以了解一下

什么是跳表

跳表（Skip List）是一种基于链表的数据结构，它可以支持快速的查找、插入、删除操作，并且具有较好的平均时间复杂度，可以替代平衡树等复杂数据结构。

跳表的由来

一、从前有一个链表，他是这样的。

他具有非常优秀的插入和删除能力，对于插入只要三步，

1、找到位置。

2、新建一个节点

3、将前面的节点指针指到新建的节点上，将新节点的指针指到后续的节点上。

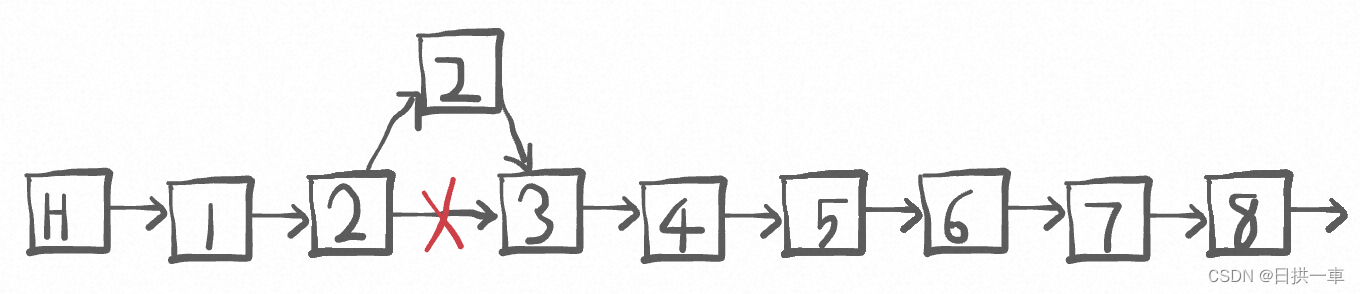
对于删除来说，只要两步。

1、找到当前节点位置，

2、将当前节点的前置节点指针指到当前节点的后续节点。

他不会像数组一样，产生碎片，需要整理。也不需要从从某个节点开始整体移动，空出地方来存储新的数据。

既然有这么优秀的特性，他却少有用武之地，这是为什么呢。

糟糕的查询

面对这么一个有序链表，我们要查询其中的某个元素，就要从头节点（H）开始便利，直到找到这个元素。对于一个有序的链表，O(n/2)的时间复杂度让他失去了有序的意义。

而且对于插入和删除的位置确定（其实也是查询），也需要从头遍历O(n/2)的时间复杂度。

大佬的优化

有一天某个大佬突然意识到，既然问题出在查询上，那么怎么优化查询呢？常见的方法就是建立索引，比如这样，我们每隔一个元素抽出来一个，这样先查索引，然后再查下面链表，不是就能节省很多时间嘛。

比如我们要查找8这个元素，按照原来的查找方法，我们需要依次访问 1->2->3->4->-5->6->7->8。按照新的数据结构，需要访问 1->3->5->7->8（

判断条件为，当前节点的下一个节点不为空且小于目标节点则往后走，否则往下走，知道找到目标元素或者最下层为空

比如要查找6，步骤如下：

显然优化了查询路径，当链表足够大时，可以看到时间复杂度从O(n/2)下降到O(n/4)。整整优化了一半。可是上面的1->3->5->7这个链表还是太长，可以继续抽取索引来优化查询，结果是这样的。

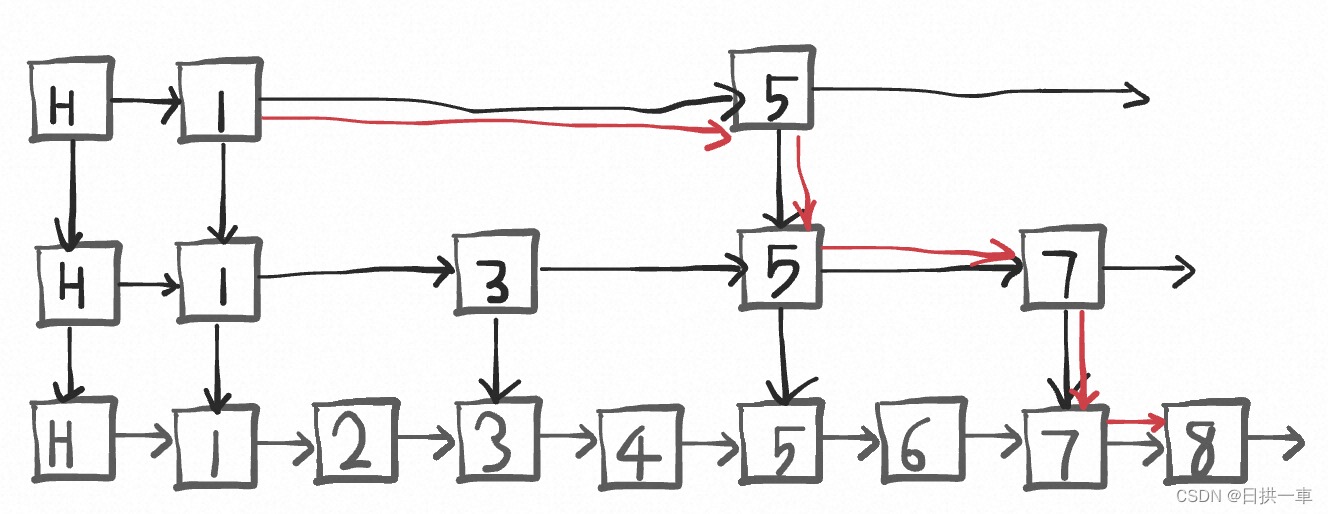
我们继续查找8这个元素，会发现路径只需要 1->5->7->8这四个元素，又优化了一步。

路径对比表如下

链表类型查询路径节点数
单链表1->2->3->4->-5->6->7->88
一级索引链表1->3->5->7->85
二级索引链表1->-5->7->84

可以看到，通过建立索引可以优化查询，弥补链表的短板。这位大佬依据这种跳过某些元素区间的查询方式，对这种数据结构起名为跳表。

时间复杂度

根据上面的定义，跳表是每层抽出一半的元素作为索引，创建多级索引来优化查询，因为上一层都是本层的一半，则有

至此一个拥有O(logN)查询复杂度兼具灵活的插入删除特性的数据结构跳表就出现了。

跳表的索引生成

上面我们说了，跳表索引最理想的生成方式是每层抽出一半作为索引，但是在涉及到插入，删除时候要平凡的改动索引，会造成很大的时间浪费，可用性不高。所以退而求其次，采用随机的方式的生成索引。虽然是随机，但是数据量越大，索引结构就会越接近理想索引。生成逻辑如下：

对于一个新加入的节点，最底层是100%插入的，所以随机数最小返回1，返回的数值代表从此层及以下都要插入索引。因为每层拿一半作为索引，所以随机数取0.5。代码如下：

public int getRandomLevel(){
        int level = 1;
        while(Math.random()<0.5&&level<MAX_LEVEL){
            level++;
        }
        return level;
    }

跳表的JAVA实现

一、定义一个链表节点

public class SkipNode<E> {
	private String key;
	private E value;
	/**
		数组存储每层索引的下一个节点。比如下标0表示链表本身，
		下标1表示第一层索引，依次类推。
	*/
	private SkipNode<E>[] next; 
	public SkipNode( String key, E value, int length ){
		this.key = key;
		this.value = value;
		next = new SkipNode[length];
	}
}

二、定义跳表的通用参数

public class SkipList<E> {
    /**
    	maxLevel 索引最大高度
    	currentLevel 当前索引高度
    	head 跳表头节点，从head查起
    */
	private int maxLevel;
	private int currentLevel;
	private SkipNode head;
	public SkipList(int maxLevel, int currentLevel){
		this.maxLevel = maxlevel;
		this.currentLevel = currentLevel
		head = new SkipNode("head",null,maxLevel);
	}
}

三、定义增删改查方法

public void insert( int key, E data ){
        SkipNode c = this.head;
        SkipNode[] update = new SkipNode[maxLevel];
        for( int i=currentLevel-1; i>=0; i--){
            while(c.next[i]!=null&&key>c.next[i].key){
                c=c.next[i];
            }
            if(c.key==key){
                c.data = data;
                return;
            }
            /**
            	记录每一层的入口节点，如果要插入索引下面会用到
            */
            update[i] = c;
        }
        int randomLevel = getRandomLevel();
        SkipNode newNode = new SkipNode(key,data,randomLevel);
        if(randomLevel>currentLevel){
            for( int i=currentLevel; i<randomLevel; i++ ){
                update[i]=this.head;
            }
            currentLevel = randomLevel;
        }
        /**
        	当前节点作为新索引节点，更新每一层的索引指向
        */
        for( int i=randomLevel-1; i>=0;i--){
            newNode.next[i] = update[i].next[i];
            update[i].next[i] = newNode;
        }
    }
    public E search( int key ){
        SkipNode<E> c = this.head;
        for( int i = currentLevel-1; i>=0; i-- ){
            while(c.next[i]!=null&&key> c.next[i].key){
                c=c.next[i];
            }
            if(c.next[i]!=null&&c.next[i].key==key){
                return c.next[i].data;
            }
        }
        return null;
    }
    public void delete( int key ){
        SkipNode skipNode = this.head;
        SkipNode[] delete = new SkipNode[currentLevel];
        for( int i=currentLevel-1; i>=0; i-- ){
            while( skipNode.next[i]!=null&&skipNode.next[i].key<key){
                skipNode = skipNode.next[i];
            }
            delete[i]=skipNode;
        }
if(delete[0].next[0]!=null&&delete[0].next[0].key==key){
            SkipNode deleteNode = delete[0].next[0];
            for( int i=0; i<currentLevel; i++ ){
                if(delete[i].next[i]==deleteNode){
                    delete[i].next[i] = delete[i].next[i].next[i];
                }
            }
      while(currentLevel>1&&this.head.next[currentLevel-1]==null){
                currentLevel--;
            }
        }
    }

到此这篇关于跳表的由来及Java实现详解的文章就介绍到这了,更多相关Java跳表内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家！

您可能感兴趣的文章:
阅读全文