揭秘Go Json.Unmarshal精度丢失之谜
作者:后端研究所
缘起
前几天写了个小需求,本来以为很简单,但是上线之后却发现出了bug。
需求大概是这样的:
- 上游调用我的服务来获取全量信息,上游的数据包虽然是json但是结构不确定
- 我的服务使用Go语言开发,所以就使用了原生的json包来进行反序列化
- 拿到唯一ID从DB拉取数据,并返回给上游调用方
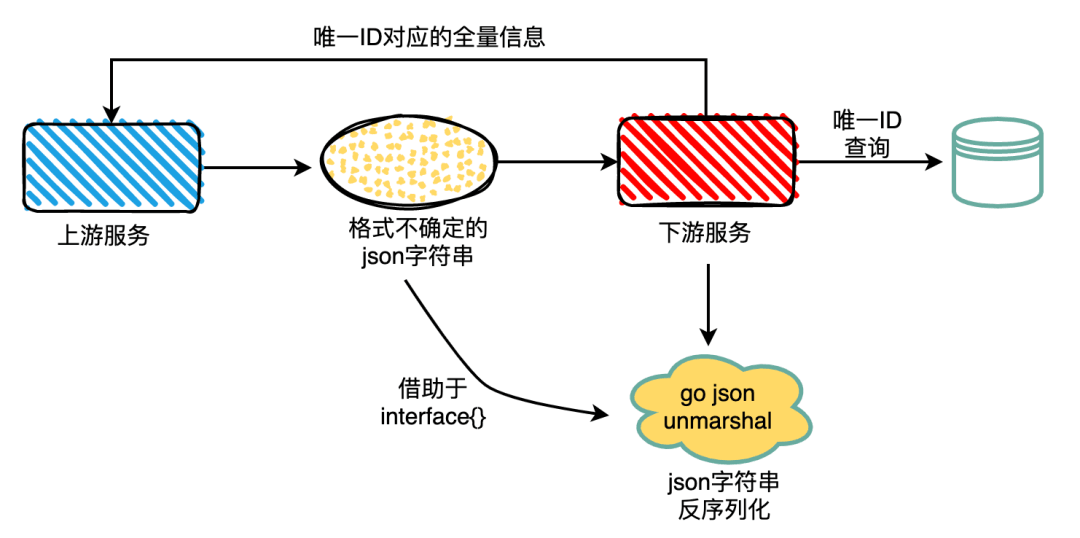
就是这么简单的过程,让我栽了个跟头,bug的现象是这样的:
- 上游给的唯一ID一直在数据库查不到结果
- 上游给的唯一ID一定是真实有效的
乖乖,这就矛盾了,于是我祭出了日志大法,在测试环境跑了一下,发现了个神奇的现象:
- 下游服务收到的json字符串中的唯一ID是没问题的,和上游一致
- 下游服务经过json.unmarshal反序列化之后唯一ID发生了变化,和上游不一致
究竟发生了什么?
难道我被智子给监控了吗?
我不理解 我不明白......
任何不合理现象背后一定有个合理的解释,千万不要像我这样被玄学占领了高地。
分析
我决定看看究竟是谁在搞鬼,现在的矛头指向了json.unmarshal这个反序列化的动作,于是我写了个小demo复现一下:
package main
import (
"encoding/json"
"fmt"
"reflect"
)
func main() {
var request = `{"id":7044144249855934983,"name":"demo"}`
var test interface{}
err := json.Unmarshal([]byte(request), &test)
if err != nil {
fmt.Println("error:", err)
}
obj := test.(map[string]interface{})
dealStr, err := json.Marshal(test)
if err != nil {
fmt.Println("error:", err)
}
id := obj["id"]
// 反序列化之后重新序列化打印
fmt.Println(string(dealStr))
fmt.Printf("%+v\n", reflect.TypeOf(id).Name())
fmt.Printf("%+v\n", id.(float64))
}跑一下看看结果如下:
{"id":7044144249855935000,"name":"demo"}
float64
7.044144249855935e+18
果然复现了:
原始输入字符串:
'{"id":7044144249855934983,"name":"demo"}'
处理后的字符串:
'{"id":7044144249855935000,"name":"demo"}'
id从7044144249855934983变成了7044144249855935000,从有效数字16位之后变为000了,所以这个id无法从db获取数据。
于是我谷歌了一波,原来是这样的:
- 在json的规范中,对于数字类型是不区分整形和浮点型的。
- 在使用json.Unmarshal进行json的反序列化的时候,如果没有指定数据类型,使用interface{}作为接收变量,其默认采用的float64作为其数字的接受类型
- 当数字的精度超过float能够表示的精度范围时就会造成精度丢失的问题
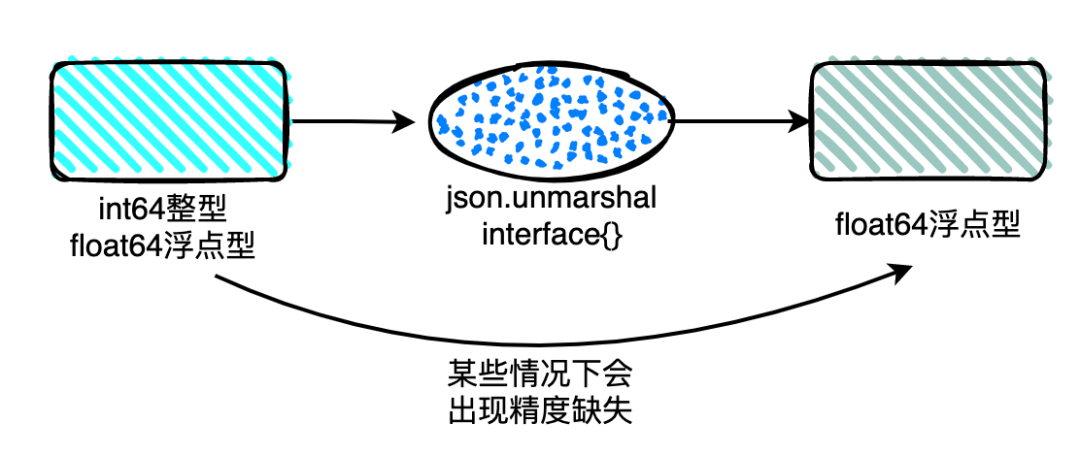
到这里,我基本清楚了为什么会出现bug:
- 上游的json字符串格式不确定无法使用struct来做反序列化,只能借助于interface{}来接收数据
- 上游的json所传的id是数值类型,换成字符串类型则没有这种问题
- 上游的json所传的id数值比较大,超过了float64的安全整数范围
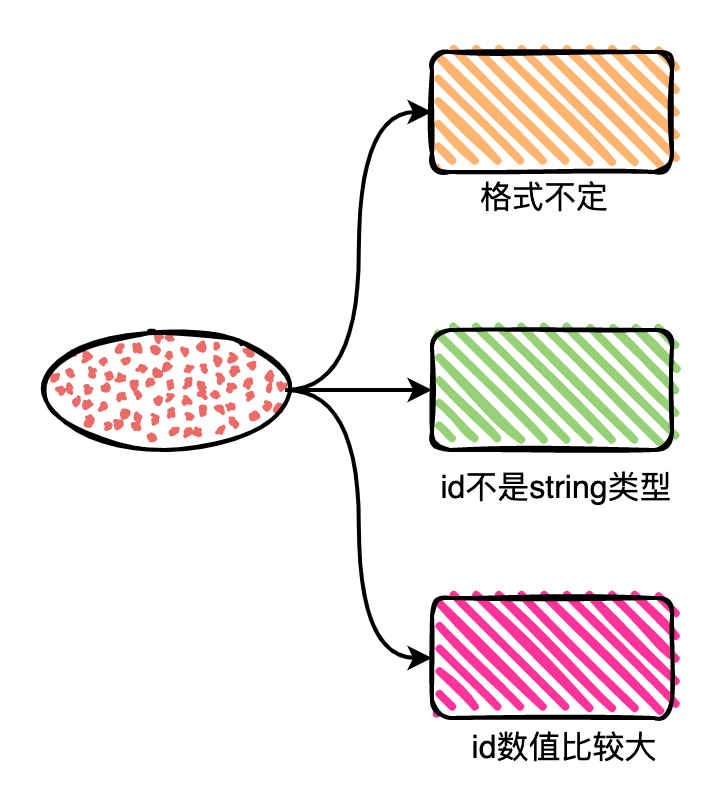
解决方案有两种:
- 上游将id改为string传给下游
- 下游使用json.number类型来避免对float64的使用
package main
import (
"encoding/json"
"fmt"
"strings"
)
func main() {
var request = `{"id":7044144249855934983}`
var test interface{}
decoder := json.NewDecoder(strings.NewReader(request))
decoder.UseNumber()
err := decoder.Decode(&test)
if err != nil {
fmt.Println("error:", err)
}
objStr, err := json.Marshal(test)
if err != nil {
fmt.Println("error:", err)
}
fmt.Println(string(objStr))
}事情到这里基本已经清晰了,改完上线就修复bug,但是我心中仍然有很多疑惑:
为什么json.unmarshal使用float64来处理就可能出现精度缺失呢?
缺失的程度是怎样的?
什么时候出现精度缺失?
里面有什么规律吗?
反序列化时decoder和unmarshal如何选择呢?
虽然问题解决了,但是没搞清楚上面这些问题,相当于并没有什么收获,于是我决定探究一番。
探究
float64作为双精度浮点型严格遵循IEEE754的标准,因此想要搞清楚为什么float64可能出现精度缺失,就必须要搞清楚二进制科学计算法和IEEE754标准的基本原理。
二进制的科学计数法
在聊float64之前,我们先回忆下十进制的科学计数法。
我们为了便于记忆和直观表达,采用科学记数法来编写数字的方法,它可以容纳太大或太小的值,在科学记数法中,所有数字都是这样编写的:x = y*10^z,此时的底数是10。
比如2000000=2*10^6,确实更加直观简便,同样的这种简化类的需求在二进制也存在,于是出现了基于二进制的科学计数法。
二进制1010010.110表示为1.010010110 × (2 ^ 6),我们后面要说的IEEE754标准本质上就是二进制科学计数法的工程标准定义。
IEEE754标准的诞生
在20世纪六七十年代,各家电脑公司的各个型号的电脑,有着千差万别的浮点数表示,却没有一个业界通用的标准。
在1980年,英特尔公司就推出了单片的8087浮点数协处理器,其浮点数表示法及定义的运算具有足够的合理性、先进性,被IEEE采用作为浮点数的标准,于1985年发布。
IEEE754(ANSI/IEEE Std 754-1985)是20世纪80年代以来最广泛使用的浮点数运算标准,为许多CPU与浮点运算器所采用,标准规定了四种表示浮点数值的方式:单精确度(32位)、双精确度(64位)、延伸单精确度(43位以上很少使用)与延伸双精确度(79位以上)。
威廉·墨顿·卡韩(英语:William Morton Kahan,1933年6月5日-),生于加拿大安大略多伦多,数学家与计算机科学家,专长于数值分析,1989年图灵奖得主,1994年被提名为ACM院士,现为加州大学柏克莱分校计算机科学名誉教授,被称为浮点数之父。
老爷子已经近90岁了,这是1968年到加州大学伯克利分校任数学与计算机科学教授时的照片。
IEEE754的基本原理
int64是将64bit的数据全部用来存储数据,但是float64需要表达的信息更多,因此float64单纯用于数据存储的位数将小于64bit,这就导致了float64可存储的最大整数是小于int64的。
理解这一点非常关键,其实也比较好理解,64bit每一位都非常重要,但是float64需要拿出其中几位来做别的事情,这样存储数据的range就比int64小了许多。

IEEE754标准将64位分为三部分:
- sign,符号位部分,1个bit 0为正数,1为负数
- exponent,指数部分,11个bit
- fraction,小数部分,52个bit
32位的单精度也分为上述三个部分,区别在于指数部分是8bit,小数部分是23bit,同时指数部分的偏移值32位是127,64位是1023,其他的部分计算规则是一样的。
IEEE754标准可以认为是二进制的科学计数法,该标准认为任何一个数字都可以表示为:
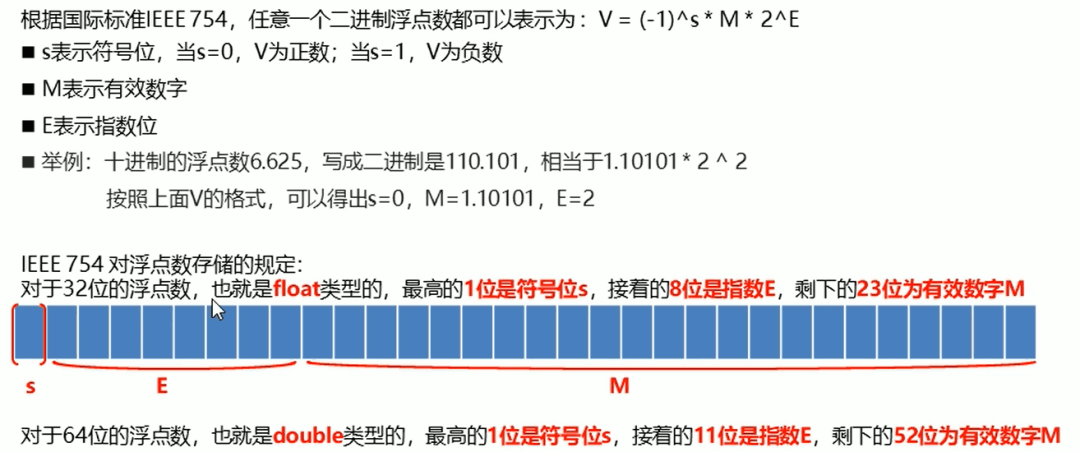
特别注意,图片中的指数部分E并没有包含偏移值,偏移值是IEEE754转换为浮点数二进制序列时使用的。
1.有效数字M的约束
M的取值为1≤M<2,M可以写成1.xxxxxx的形式,其中xxxxxx表示小数部分。IEEE 754规定,在计算机内部保存M时,默认这个数的第一位总是1,因此可以被舍去,只保存后面的xxxxxx部分,在恢复计算时加上1即可。
2.指数E的约束
E为一个无符号整数也就是都是>=0,在32位单精度时取值范围为0~255,在64位双精度时取值范围为0~2047。当数字是小数时E将是负数,为此IEEE754规定使用科学计数法求的真实E加上偏移值才是最终表示的E值。
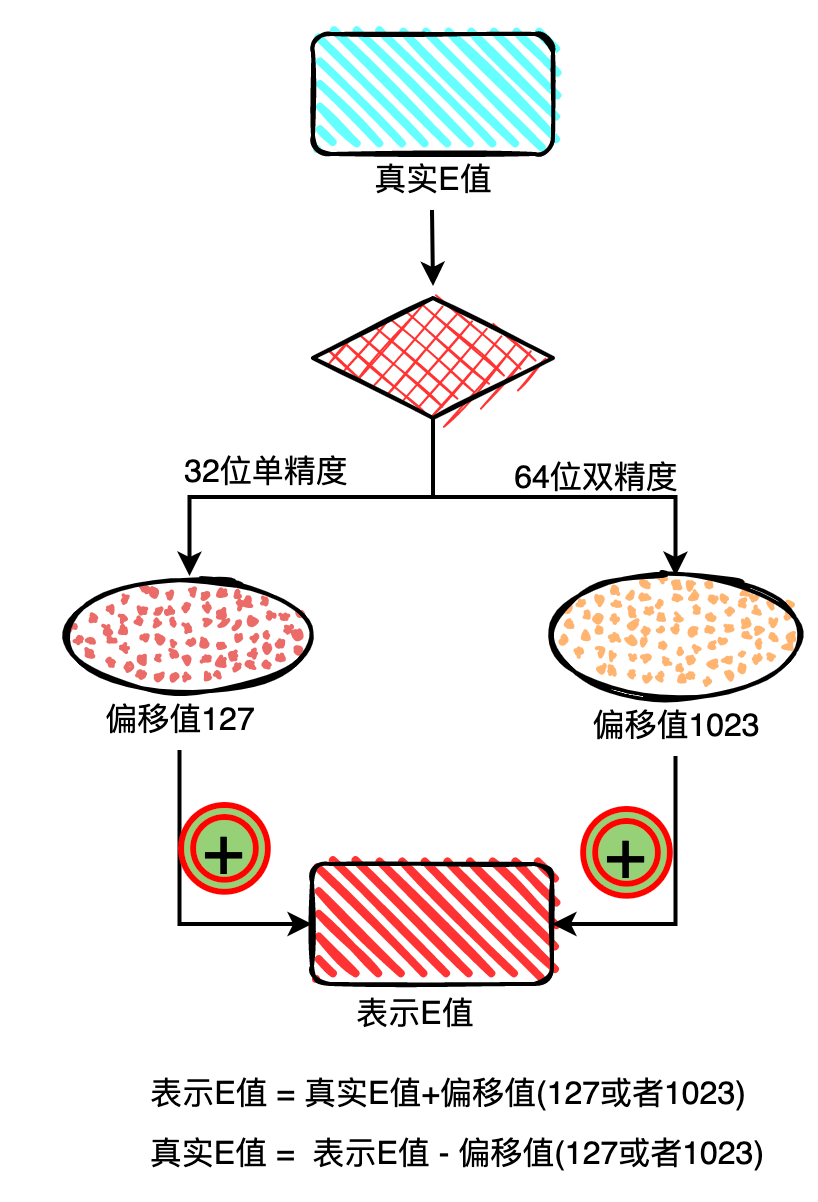
看到这里读者会有疑问:如果真实E值超过128,那么加上偏移值岂不是要超过255发生越界了?
没错,当指数部分E全部为1时,需要看M的情况,如果有效数字M全为0,表示±无穷大,如果有效数字M不全为0,表示为NaN。
NaN(Not a Number非数)是计算机科学中数值数据类型的一类值,含义为未定义或不可表示的值。
数据表示规则
前面了解了IEEE754的基本原理,接下来就是实际应用了。
一般来说10进制场景下存在三种情况转换为浮点型:
- 纯整数转换为浮点数 比如 10086
- 混合小数转换为浮点数 比如 123.45
- 纯小数转换为浮点数 比如 0.12306
就分为两种情况将10进制全部转换为2进制就可以了,比如整数部分123就辗转除2取余数再逆向书写就好,小数部分则是辗转乘2取整再顺序书写就好。
偷个懒从菜鸟教程网站上copy个例子,将10进制173.8625转换为2进制的做法:
十进制整数转换为二进制整数采用"除2取余,逆序排列"法
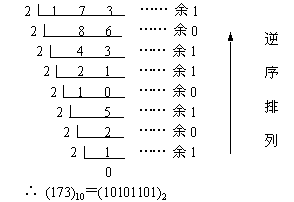
十进制小数转换成二进制小数采用"乘2取整,顺序排列"法
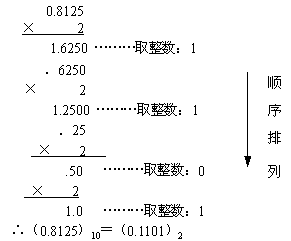
合并两部分
(173.8125)10=(10101101.1101)2
特别注意,在某些情况下小数部分的乘2取整会出现无限循环,但是IEEE754中小数部分的位数是有限的,这样就出现了近似值存储,这也是一种精度缺失的现象。
安全整数范围
我们之前有疑问:任何整数经过float64处理后都有问题吗?还是说有个安全转换的数值范围呢?
我们来分析下float64可以表示的数据范围是怎样的:

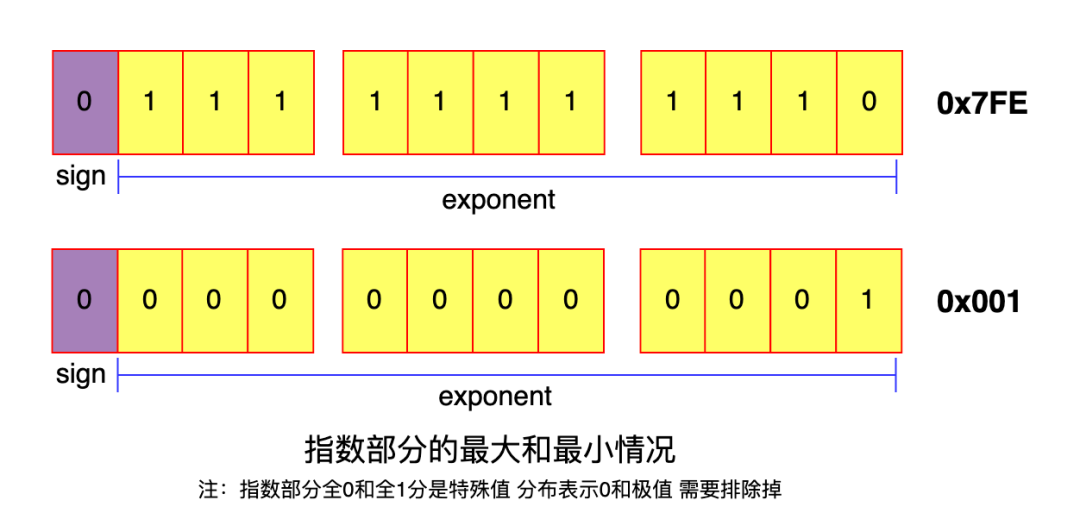
尾数部分全部为1时就已经拉满了,再多1位尾数就要向指数发生进位,此时就会出现精度缺失,因此对于float64来说:
- 最大的安全整数是52位尾数全为1且指数部分为最小 0x001F FFFF FFFF FFFF
- float64可以存储的最大整数是52位尾数全位1且指数部分为最大 0x07FEF FFFF FFFF FFFF
(0x001F FFFF FFFF FFFF)16 = (9007199254740991)10
(0x07EF FFFF FFFF FFFF)16 = (9218868437227405311)10
也就是理论上数值超过9007199254740991就可能会出现精度缺失。
10进制数值的有效数字是16位,一旦超过16位基本上缺失精度是没跑了,回过头看我处理的id是20位长度,所以必然出现精度缺失。
decoder和unmarshal
我们知道在json反序列化时是没有整型和浮点型的区别,数字都使用同一种类型,在go语言的类型中这种共同类型就是float64。
但是float64存在精度缺失的问题,因此go单独对此给出了一个解决方案:
- 使用 json.Decoder 来代替 json.Unmarshal 方法
- 该方案首先创建了一个 jsonDecoder,然后调用了 UseNumber 方法
- 使用 UseNumber 方法后,json 包会将数字转换成一个内置的 Number 类型(本质是string),Number类型提供了转换为 int64、float64 等多个方法
UseNumber causes the Decoder to unmarshal a number into an interface{} as a Number instead of as a float64
我们来看看Number类型的源码实现:
// A Number represents a JSON number literal.
type Number string
// String returns the literal text of the number.
func (n Number) String() string { return string(n) }
// Float64 returns the number as a float64.
func (n Number) Float64() (float64, error) {
return strconv.ParseFloat(string(n), 64)
}
// Int64 returns the number as an int64.
func (n Number) Int64() (int64, error) {
return strconv.ParseInt(string(n), 10, 64)
}从上面可以看到json包的NewDecoder和unmarshal都可以实现数据的解析,那么二者有何区别,什么时候选择哪种方法呢?
其中的高赞答案给出了一些观点:
- json.NewDecoder是从一个流里面直接进行解码,代码更少,可以用于http连接与socket连接的读取与写入,或者文件读取
- json.Unmarshal是从已存在与内存中的json进行解码
小结
到这里大部分问题已经搞清楚,但是仍然一些疑问没有搞清楚:
- 为什么json.unmarshal没有直接只用类似于decode方案中的Number类型来避免float64带来的精度损失?
- json.unmarshal反序列化过程的详细原理是怎样的?
以上就是揭秘Go Json.Unmarshal精度丢失之谜的详细内容,更多关于go json.Unmarshal的资料请关注脚本之家其它相关文章!
