JavaScript 浮点数精度问题小结
作者:前端梦工厂+
一. 引言
浮点数精度问题是指在计算机中使用二进制表示浮点数时,由于二进制无法精确表示某些十进制小数,导致计算结果可能存在舍入误差或不精确的情况。
这个问题主要源于浮点数的存储方式。在计算机中,浮点数通常使用IEEE 754标准来表示。该标准将浮点数分为符号位、指数位和尾数位,使用科学计数法来表示一个浮点数。
二. 常见浮点数精度问题
1. 示例一:浮点值运算结果
// 加法 console.log(0.1 + 0.2); // 0.30000000000000004 console.log(0.7 + 0.1); // 0.7999999999999999 console.log(0.2 + 0.4); // 0.6000000000000001 console.log(2.22 + 0.1); // 2.3200000000000003 // 减法 console.log(1.5 - 1.2); // 0.30000000000000004 console.log(0.3 - 0.2); // 0.09999999999999998 // 乘法 console.log(19.9 * 100); // 1989.9999999999998 console.log(19.9 * 10 * 10); // 1990 console.log(9.7 * 100); // 969.9999999999999 console.log(39.7 * 100); // 3970.0000000000005 // 除法 console.log(0.3 / 0.1); // 2.9999999999999996 console.log(0.69 / 10); // 0.06899999999999999
运行结果如下图所示:
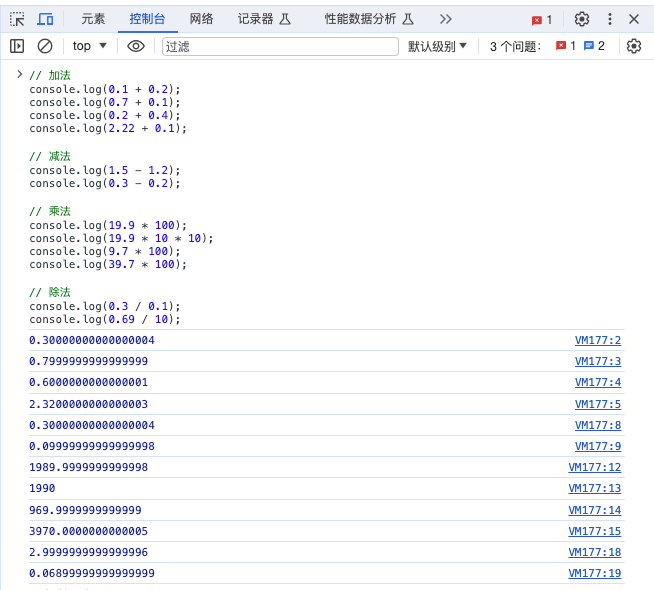
2. 示例二:小数乘以10的n次方取整(比如:元转分,米转厘米)
console.log(parseInt(0.58 * 100, 10)); // 57
在上面的例子中,我们得出的结果是 57,而不是预期结果 58。
3. 示例三:四舍五入保留 n 位小数
例如我们会写出 (number).toFixed(2) ,但是看下面的例子:
console.log((1.335).toFixed(2)); // 1.33
在上面的例子中,我们得出的结果是 1.33,而不是预期结果 1.34。
三. 为什么会出现这样的结果
1. 浮点数表示
在计算机中,浮点数通常使用IEEE 754标准来表示。该标准将浮点数分为符号位、指数位和尾数位,使用科学计数法来表示一个浮点数。
该规范定义了浮点数的格式,对于 64 位的浮点数在内存中的表示,最高的 1 位是符号位,接着的 11 位是指数,剩下的 52 位为有效数字,具体表示方式如下:
符号位 S:用于表示正负号。第 1 位是正负数符号位(sign),0 代表正数,1 代表负数。
指数位 E:用于表示浮点数的指数部分,以二进制补码形式存储。中间的 11 位存储指数(exponent),用来表示次方数。
尾数位 M:用于表示浮点数的有效数字部分,以二进制形式存储。最后的 52 位是尾数(mantissa),储存小数部分,超出的部分自动进一舍零。
即:浮点数最终在运算的时候实际上是一个符合该标准的二进制数
符号位决定了一个数的正负,指数部分决定了数值的大小,小数部分决定了数值的精度。
IEEE 754 规定,有效数字第一位默认总是 1,不保存在 64 位浮点数之中。也就是说,有效数字总是 1.xx…xx 的形式,其中 xx…xx 的部分保存在 64 位浮点数之中,最长可能为 52 位。因此,JavaScript 提供的有效数字最长为 53 个二进制位(64 位浮点的后 52 位 + 有效数字第一位的 1)。
既然限定位数,必然有截断的可能。
2. 举例说明
示例一
console.log(0.1 + 0.2); // 0.30000000000000004
为了验证该例子,我们得先知道怎么将浮点数转换为二进制,整数我们可以用除 2 取余的方式,小数我们则可以用乘 2 取整的方式。
*0.1* 转换为二进制
0.1 * 2,值为 0.2,小数部分 0.2,整数部分 0
0.2 * 2,值为 0.4,小数部分 0.4,整数部分 0
0.4 * 2,值为 0.8,小数部分 0.8,整数部分 0
0.8 * 2,值为 1.6,小数部分 0.6,整数部分 1
0.6 * 2,值为 1.2,小数部分 0.2,整数部分 1
0.2 * 2,值为 0.4,小数部分 0.4,整数部分 0
从 0.2 开始循环
*0.2* 转换为二进制
可以直接参考上述,肯定最后也是一个循环的情况
所以最终我们能得到两个循环的二进制数:
0.1:0.0001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1100 ...
0.2:0.0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 ...
这两个的和的二进制就是:
sum:0.0100 1100 1100 1100 1100 1100 1100 1100 1100 1100 1100 1100 1100 1100 ...
最终我们只能得到和的近似值(按照 IEEE 754 标准保留 52 位,按 0 舍 1 入来取值),然后转换为十进制数变成:
sum ≈ 0.30000000000000004
示例二
console.log((1.335).toFixed(2)); // 1.33
因为 1.335 其实是 1.33499999999999996447286321199,toFixed 虽然是四舍五入,但是是对 1.33499999999999996447286321199 进行四五入,所以得出 1.33。
示例三
在 Javascript 中,整数精度同样存在问题,先来看看问题:
console.log(19571992547450991) // 19571992547450990 console.log(19571992547450991 === 19571992547450992) // true
如下图所示:

同样的原因,在 JavaScript 中 number 类型统一按浮点数处理,整数是按最大 54 位来算。
最大( 253 - 1,Number.MAX_SAFE_INTEGER、9007199254740991)
最小( -(253 - 1) ,Number.MIN_SAFE_INTEGER、*-9007199254740991*)
在浮点数计算中,有一些特定的小数情况可以避免舍入误差。这是因为这些特定的小数可以精确地表示为二进制分数,而不会导致舍入误差。以下是一些常见的特定情况:
小数部分是2的负整数次幂:例如,0.5、0.25、0.125等。这些小数在二进制中可以精确表示,因此计算时不会出现舍入误差。
小数部分是10的负整数次幂:例如,0.1、0.01、0.001等。尽管在十进制中无法精确表示,但在二进制中可以通过有限位数进行近似表示,并且通常不会引起明显的舍入误差。
四. 总结
浮点数精度问题是计算机科学中一个常见的问题,由于二进制无法精确表示某些十进制小数,进行浮点数运算时可能会出现舍入误差。为了解决这个问题,可以使用整数进行计算、使用专门的库或者比较时使用误差范围。了解浮点数精度问题对于开发人员在处理浮点数运算时具有重要意义。
到此这篇关于JavaScript 浮点数精度问题小结的文章就介绍到这了,更多相关JavaScript 浮点数精度内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家!
