C++实现八个常用的排序算法 插入排序、冒泡排序、选择排序、希尔排序等
作者:Terry_小三哥
这篇文章主要介绍了C++如何实现八个常用的排序算法:插入排序、冒泡排序、选择排序、希尔排序 、快速排序、归并排序、堆排序和LST基数排序,需要的朋友可以参考下
本文实现了八个常用的排序算法:插入排序、冒泡排序、选择排序、希尔排序 、快速排序、归并排序、堆排序和LST基数排序
首先是算法实现文件Sort.h,代码如下:
/*
* 实现了八个常用的排序算法:插入排序、冒泡排序、选择排序、希尔排序
* 以及快速排序、归并排序、堆排序和LST基数排序
* @author gkh178
*/
#include <iostream>
template<class T>
void swap_value(T &a, T &b)
{
T temp = a;
a = b;
b = temp;
}
//插入排序:时间复杂度o(n^2)
template<class T>
void insert_sort(T a[], int n)
{
for (int i = 1; i < n; ++i)
{
T temp = a[i];
int j = i - 1;
while (j >= 0 && a[j] > temp)
{
a[j + 1] = a[j];
--j;
}
a[j + 1] = temp;
}
}
//冒泡排序:时间复杂度o(n^2)
template<class T>
void bubble_sort(T a[], int n)
{
for (int i = n - 1; i > 0; --i)
{
for (int j = 0; j < i; ++j)
{
if (a[j] > a[j + 1])
{
swap_value(a[j], a[j + 1]);
}
}
}
}
//选择排序:时间复杂度o(n^2)
template<class T>
void select_sort(T a[], int n)
{
for (int i = 0; i < n - 1; ++i)
{
T min = a[i];
int index = i;
for (int j = i + 1; j < n; ++j)
{
if (a[j] < min)
{
min = a[j];
index = j;
}
}
a[index] = a[i];
a[i] = min;
}
}
//希尔排序:时间复杂度介于o(n^2)和o(nlgn)之间
template<class T>
void shell_sort(T a[], int n)
{
for (int gap = n / 2; gap >= 1; gap /= 2)
{
for (int i = gap; i < n; ++i)
{
T temp = a[i];
int j = i - gap;
while (j >= 0 && a[j] > temp)
{
a[j + gap] = a[j];
j -= gap;
}
a[j + gap] = temp;
}
}
}
//快速排序:时间复杂度o(nlgn)
template<class T>
void quick_sort(T a[], int n)
{
_quick_sort(a, 0, n - 1);
}
template<class T>
void _quick_sort(T a[], int left, int right)
{
if (left < right)
{
int q = _partition(a, left, right);
_quick_sort(a, left, q - 1);
_quick_sort(a, q + 1, right);
}
}
template<class T>
int _partition(T a[], int left, int right)
{
T pivot = a[left];
while (left < right)
{
while (left < right && a[right] >= pivot)
{
--right;
}
a[left] = a[right];
while (left < right && a[left] <= pivot)
{
++left;
}
a[right] = a[left];
}
a[left] = pivot;
return left;
}
//归并排序:时间复杂度o(nlgn)
template<class T>
void merge_sort(T a[], int n)
{
_merge_sort(a, 0, n - 1);
}
template<class T>
void _merge_sort(T a[], int left, int right)
{
if (left < right)
{
int mid = left + (right - left) / 2;
_merge_sort(a, left, mid);
_merge_sort(a, mid + 1, right);
_merge(a, left, mid, right);
}
}
template<class T>
void _merge(T a[], int left, int mid, int right)
{
int length = right - left + 1;
T *newA = new T[length];
for (int i = 0, j = left; i <= length - 1; ++i, ++j)
{
*(newA + i) = a[j];
}
int i = 0;
int j = mid - left + 1;
int k = left;
for (; i <= mid - left && j <= length - 1; ++k)
{
if (*(newA + i) < *(newA + j))
{
a[k] = *(newA + i);
++i;
}
else
{
a[k] = *(newA + j);
++j;
}
}
while (i <= mid - left)
{
a[k++] = *(newA + i);
++i;
}
while (j <= right - left)
{
a[k++] = *(newA + j);
++j;
}
delete newA;
}
//堆排序:时间复杂度o(nlgn)
template<class T>
void heap_sort(T a[], int n)
{
built_max_heap(a, n);//建立初始大根堆
//交换首尾元素,并对交换后排除尾元素的数组进行一次上调整
for (int i = n - 1; i >= 1; --i)
{
swap_value(a[0], a[i]);
up_adjust(a, i);
}
}
//建立一个长度为n的大根堆
template<class T>
void built_max_heap(T a[], int n)
{
up_adjust(a, n);
}
//对长度为n的数组进行一次上调整
template<class T>
void up_adjust(T a[], int n)
{
//对每个带有子女节点的元素遍历处理,从后到根节点位置
for (int i = n / 2; i >= 1; --i)
{
adjust_node(a, n, i);
}
}
//调整序号为i的节点的值
template<class T>
void adjust_node(T a[], int n, int i)
{
//节点有左右孩子
if (2 * i + 1 <= n)
{
//右孩子的值大于节点的值,交换它们
if (a[2 * i] > a[i - 1])
{
swap_value(a[2 * i], a[i - 1]);
}
//左孩子的值大于节点的值,交换它们
if (a[2 * i - 1] > a[i - 1])
{
swap_value(a[2 * i - 1], a[i - 1]);
}
//对节点的左右孩子的根节点进行调整
adjust_node(a, n, 2 * i);
adjust_node(a, n, 2 * i + 1);
}
//节点只有左孩子,为最后一个有左右孩子的节点
else if (2 * i == n)
{
//左孩子的值大于节点的值,交换它们
if (a[2 * i - 1] > a[i - 1])
{
swap_value(a[2 * i - 1], a[i - 1]);
}
}
}
//基数排序的时间复杂度为o(distance(n+radix)),distance为位数,n为数组个数,radix为基数
//本方法是用LST方法进行基数排序,MST方法不包含在内
//其中参数radix为基数,一般为10;distance表示待排序的数组的数字最长的位数;n为数组的长度
template<class T>
void lst_radix_sort(T a[], int n, int radix, int distance)
{
T* newA = new T[n];//用于暂存数组
int* count = new int[radix];//用于计数排序,保存的是当前位的值为0 到 radix-1的元素出现的的个数
int divide = 1;
//从倒数第一位处理到第一位
for (int i = 0; i < distance; ++i)
{
//待排数组拷贝到newA数组中
for (int j = 0; j < n; ++j)
{
*(newA + j) = a[j];
}
//将计数数组置0
for (int j = 0; j < radix; ++j)
{
*(count + j) = 0;
}
for (int j = 0; j < n; ++j)
{
int radixKey = (*(newA + j) / divide) % radix; //得到数组元素的当前处理位的值
(*(count + radixKey))++;
}
//此时count[]中每个元素保存的是radixKey位出现的次数
//计算每个radixKey在数组中的结束位置,位置序号范围为1-n
for (int j = 1; j < radix; ++j)
{
*(count + j) = *(count + j) + *(count + j - 1);
}
//运用计数排序的原理实现一次排序,排序后的数组输出到a[]
for (int j = n - 1; j >= 0; --j)
{
int radixKey = (*(newA + j) / divide) % radix;
a[*(count + radixKey) - 1] = newA[j];
--(*(count + radixKey));
}
divide = divide * radix;
}
}
然后是测试文件main.cpp,代码如下:
#include "Sort.h"
using namespace std;
template<class T>
void printArray(T a[], int n)
{
for (int i = 0; i < n; ++i)
{
cout << a[i] << " ";
}
cout << endl;
}
int main()
{
for (int i = 1; i <= 8; ++i)
{
int arr[] = { 45, 38, 26, 77, 128, 38, 25, 444, 61, 153, 9999, 1012, 43, 128 };
switch (i)
{
case 1:
insert_sort(arr, sizeof(arr) / sizeof(arr[0]));
break;
case 2:
bubble_sort(arr, sizeof(arr) / sizeof(arr[0]));
break;
case 3:
select_sort(arr, sizeof(arr) / sizeof(arr[0]));
break;
case 4:
shell_sort(arr, sizeof(arr) / sizeof(arr[0]));
break;
case 5:
quick_sort(arr, sizeof(arr) / sizeof(arr[0]));
break;
case 6:
merge_sort(arr, sizeof(arr) / sizeof(arr[0]));
break;
case 7:
heap_sort(arr, sizeof(arr) / sizeof(arr[0]));
break;
case 8:
lst_radix_sort(arr, sizeof(arr) / sizeof(arr[0]), 10, 4);
break;
default:
break;
}
printArray(arr, sizeof(arr) / sizeof(arr[0]));
}
return 0;
}
最后是运行结果图,如下:
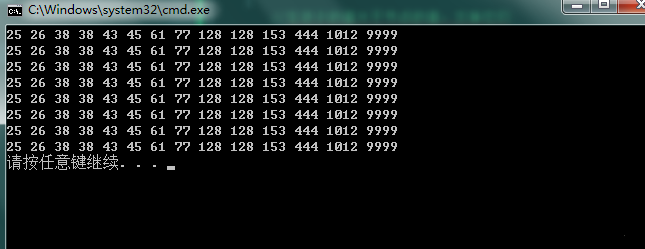
以上就是C++实现八个常用的排序算法的全部代码,希望大家对C++排序算法有更进一步的了解。
