PyTorch中的神经网络 Mnist 分类任务
作者:虚心求知的熊
这篇文章主要介绍了PyTorch中的神经网络 Mnist 分类任务,在本次的分类任务当中,我们使用的数据集是 Mnist 数据集,这个数据集大家都比较熟悉,需要的朋友可以参考下
本文参加新星计划人工智能(Pytorch)赛道:https://bbs.csdn.net/topics/613989052

一、Mnist 分类任务简介
- 在上一篇博客当中,我们通过搭建 PyTorch 神经网络实现了气温预测,这本质上是一个回归任务。在本次博文当中,我们使用 PyTorch 做一个分类任务。
- 其实,分类任务和回归任务在本质上没有任何区别,只是说在结果上是不同的,损失函数是不同的,中间的网络架构却是大体一致的。
- 在本次的分类任务当中,我们使用的数据集是 Mnist 数据集,这个数据集大家都比较熟悉,可以在 http://yann.lecun.com/exdb/mnist/ 中获取,主要包括四个文件:
| 文件名称 | 大小 | 内容 |
|---|---|---|
| train-images-idx3-ubyte.gz | 9,681 kb | 55000 张训练集,5000 张验证集 |
| train-labels-idx1-ubyte.gz | 29 kb | 训练集图片对应的标签 |
| t10k-images-idx3-ubyte.gz | 1,611kb | 10000 张测试集 |
| t10k-labels-idx1-ubyte.gz | 5 kb | 测试集图片对应的标签 |
- 在上述在上述文件中,训练集 train 一共包含了 60000 张图像和标签,而测试集一共包含了 10000 张图像和标签。
- idx3 表示 3 维,ubyte 表示是以字节的形式进行存储的,t10k 表示 10000 张测试图片(test10000)。
- 每张图片是一个 28*28 像素点的 0 ~ 9 的灰质手写数字图片,黑底白字,图像像素值为 0 ~ 255,越大该点越白。
- 本次分类任务主要包含如下的几个部分:
- (1) 网络基本构建与训练方法,常用函数解析。
- (2) torch.nn.functional 模块。
- (3) nn.Module 模块。
二、Mnist 数据集的读取
- 对于 Mnist 数据集,我们可以通过代码编写,就可以实现自动下载。
%matplotlib inline
from pathlib import Path
import requests
DATA_PATH = Path("data")
PATH = DATA_PATH / "mnist"
PATH.mkdir(parents=True, exist_ok=True)
URL = "http://deeplearning.net/data/mnist/"
FILENAME = "mnist.pkl.gz"对于我们上面定义的下载路径等等,会进行自动判断,如果该路径下没有 Minst 数据集的话,就会自动进行下载。
if not (PATH / FILENAME).exists():
content = requests.get(URL + FILENAME).content
(PATH / FILENAME).open("wb").write(content)由于下载出来的数据集是压缩包的状态,因此,我们还需要对其进行解压,具体的代码详见下面。
import pickle
import gzip
with gzip.open((PATH / FILENAME).as_posix(), "rb") as f:
((x_train, y_train), (x_valid, y_valid), _) = pickle.load(f, encoding="latin-1")在上述工作准备完成后,我们可以先查看一个数据,观察他的特征。
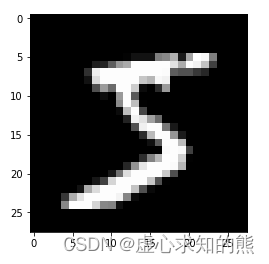
from matplotlib import pyplot import numpy as np pyplot.imshow(x_train[0].reshape((28, 28)), cmap="gray") print(x_train.shape) #(50000, 784)
在此处,我们查看的训练集当中的第一个数据,大小重构为 (28,28,1),表示长是 28,宽是 28,颜色通道是 1(黑白图就只有一个颜色通道),颜色设置为灰色。在查看第一个数据的同时,我们也输出整个训练集的数据大小,其中,(50000, 784) 中的 50000 表示训练集一共有 50000 个数据样本,784 表示训练集中每个样本有 784 个像素点(可以理解成 784 个特征)。
三、 Mnist 分类任务实现
1. 标签和简单网络架构 在分类任务当中,标签的设计是有所不同的。
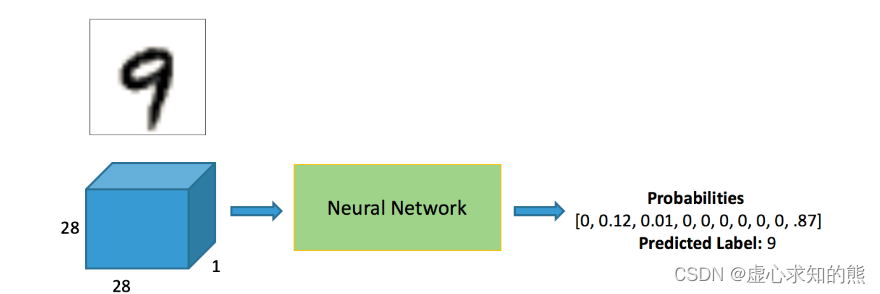
- 很多人认为预测出来的 9,具体指的是 0,1,2,3,4,5,6,7,8,9 当中的具体哪一个,但实际上并不是这样的,他也是一个 One-Hot 的编码,他预测的出来的不是一个具体的数值,而是十个概率,就是当前这个输入属于 0-9 这十个数字的概率是多少。
- 以上图为例,该输入属于 0 的概率就是 0,属于 1 的概率就是 12%,属于 9 的概率就是 87%,属于 9 的概率最高,因此,该输入的输出就是 9。
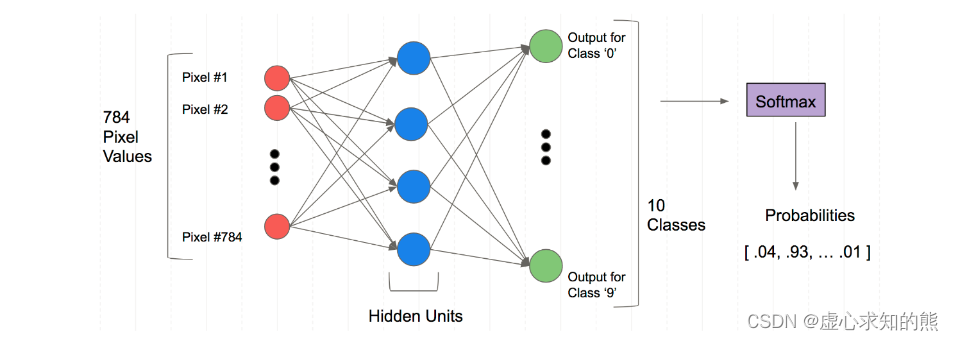
- 对于这个网络架构,由于我们的每个数据样本都有 784 个像素点,中间进行特征提取,得到一定数量的特征,最终得到 10 个输出,通过 Softmax 层得到是个概率。
2. 具体代码实现
- 需要注意的是,我们需要先将数据转换成 tensor 才能参与后续建模训练。
- 这里的数据包括 x_train, y_train, x_valid, y_valid 四种,对于他们的含义,我们可以这样理解:
- (1) x_train 包括所有自变量,这些变量将用于训练模型。
- (2) y_train 是指因变量,需要此模型进行预测,其中包括针对自变量的类别标签,我们需要在训练/拟合模型时指定我们的因变量。
- (3) x_valid 也就是 x_test,这些自变量将不会在训练阶段使用,并将用于进行预测,以测试模型的准确性。
- (4) y_valid 也就是 y_test,此数据具有测试数据的类别标签,这些标签将用于测试实际类别和预测类别之间的准确性。
import torch
x_train, y_train, x_valid, y_valid = map(
torch.tensor, (x_train, y_train, x_valid, y_valid)
)
n, c = x_train.shape
x_train, x_train.shape, y_train.min(), y_train.max()
print(x_train, y_train)
print(x_train.shape)
print(y_train.min(), y_train.max())
#tensor([[0., 0., 0., ..., 0., 0., 0.],
# [0., 0., 0., ..., 0., 0., 0.],
# [0., 0., 0., ..., 0., 0., 0.],
# ...,
# [0., 0., 0., ..., 0., 0., 0.],
# [0., 0., 0., ..., 0., 0., 0.],
# [0., 0., 0., ..., 0., 0., 0.]]) tensor([5, 0, 4, ..., 8, 4, 8])
#torch.Size([50000, 784])
#tensor(0) tensor(9)- 在模型训练的过程中,大家经常会看到 nn.Module 和 nn.functional。那什么时候使用 nn.Module,什么时候使用 nn.functional 呢?
- 一般情况下,如果模型有可学习的参数,最好用 nn.Module,其他情况 nn.functional 相对更简单一些。
- 我们先导入需要的模块包。
import torch.nn.functional as F
loss_func = F.cross_entropy
def model(xb):
return xb.mm(weights) + bias然后进行参数的设定。
bs = 64 xb = x_train[0:bs] # a mini-batch from x yb = y_train[0:bs] weights = torch.randn([784, 10], dtype = torch.float, requires_grad = True) bs = 64 bias = torch.zeros(10, requires_grad=True) print(loss_func(model(xb), yb)) #tensor(10.7988, grad_fn=<NllLossBackward>)
- 我们也创建一个 model 来更简化代码。
- 在这中间必须继承 nn.Module 且在其构造函数中需调用 nn.Module 的构造函数,无需写反向传播函数,nn.Module 能够利用 autograd 自动实现反向传播,Module 中的可学习参数可以通过 named_parameters() 或者 parameters() 返回迭代器。
from torch import nn
class Mnist_NN(nn.Module):
def __init__(self):
super().__init__()
self.hidden1 = nn.Linear(784, 128) #隐藏层1:784*128
self.hidden2 = nn.Linear(128, 256) #隐藏层2:128*256
self.out = nn.Linear(256, 10) #输出层,256*10
def forward(self, x):
x = F.relu(self.hidden1(x))
x = F.relu(self.hidden2(x))
x = self.out(x)
return x
net = Mnist_NN()
print(net)
#Mnist_NN(
# (hidden1): Linear(in_features=784, out_features=128, bias=True)
# (hidden2): Linear(in_features=128, out_features=256, bias=True)
# (out): Linear(in_features=256, out_features=10, bias=True)
#)我们可以打印定义好名字里的权重和偏置项,首先打印名字,然后打印参数,最后打印参数的维度。
for name, parameter in net.named_parameters():
print(name, parameter,parameter.size())
#hidden1.weight Parameter containing:
#tensor([[ 0.0018, 0.0218, 0.0036, ..., -0.0286, -0.0166, 0.0089],
# [-0.0349, 0.0268, 0.0328, ..., 0.0263, 0.0200, -0.0137],
# [ 0.0061, 0.0060, -0.0351, ..., 0.0130, -0.0085, 0.0073],
# ...,
# [-0.0231, 0.0195, -0.0205, ..., -0.0207, -0.0103, -0.0223],
# [-0.0299, 0.0305, 0.0098, ..., 0.0184, -0.0247, -0.0207],
# [-0.0306, -0.0252, -0.0341, ..., 0.0136, -0.0285, 0.0057]],
# requires_grad=True) torch.Size([128, 784])
#hidden1.bias Parameter containing:
#tensor([ 0.0072, -0.0269, -0.0320, -0.0162, 0.0102, 0.0189, -0.0118, -0.0063,
# -0.0277, 0.0349, 0.0267, -0.0035, 0.0127, -0.0152, -0.0070, 0.0228,
# -0.0029, 0.0049, 0.0072, 0.0002, -0.0356, 0.0097, -0.0003, -0.0223,
# -0.0028, -0.0120, -0.0060, -0.0063, 0.0237, 0.0142, 0.0044, -0.0005,
# 0.0349, -0.0132, 0.0138, -0.0295, -0.0299, 0.0074, 0.0231, 0.0292,
# -0.0178, 0.0046, 0.0043, -0.0195, 0.0175, -0.0069, 0.0228, 0.0169,
# 0.0339, 0.0245, -0.0326, -0.0260, -0.0029, 0.0028, 0.0322, -0.0209,
# -0.0287, 0.0195, 0.0188, 0.0261, 0.0148, -0.0195, -0.0094, -0.0294,
# -0.0209, -0.0142, 0.0131, 0.0273, 0.0017, 0.0219, 0.0187, 0.0161,
# 0.0203, 0.0332, 0.0225, 0.0154, 0.0169, -0.0346, -0.0114, 0.0277,
# 0.0292, -0.0164, 0.0001, -0.0299, -0.0076, -0.0128, -0.0076, -0.0080,
# -0.0209, -0.0194, -0.0143, 0.0292, -0.0316, -0.0188, -0.0052, 0.0013,
# -0.0247, 0.0352, -0.0253, -0.0306, 0.0035, -0.0253, 0.0167, -0.0260,
# -0.0179, -0.0342, 0.0033, -0.0287, -0.0272, 0.0238, 0.0323, 0.0108,
# 0.0097, 0.0219, 0.0111, 0.0208, -0.0279, 0.0324, -0.0325, -0.0166,
# -0.0010, -0.0007, 0.0298, 0.0329, 0.0012, -0.0073, -0.0010, 0.0057],
# requires_grad=True) torch.Size([128])
#hidden2.weight Parameter containing:
#tensor([[-0.0383, -0.0649, 0.0665, ..., -0.0312, 0.0394, -0.0801],
# [-0.0189, -0.0342, 0.0431, ..., -0.0321, 0.0072, 0.0367],
# [ 0.0289, 0.0780, 0.0496, ..., 0.0018, -0.0604, -0.0156],
# ...,
# [-0.0360, 0.0394, -0.0615, ..., 0.0233, -0.0536, -0.0266],
# [ 0.0416, 0.0082, -0.0345, ..., 0.0808, -0.0308, -0.0403],
# [-0.0477, 0.0136, -0.0408, ..., 0.0180, -0.0316, -0.0782]],
# requires_grad=True) torch.Size([256, 128])
#hidden2.bias Parameter containing:
#tensor([-0.0694, -0.0363, -0.0178, 0.0206, -0.0875, -0.0876, -0.0369, -0.0386,
# 0.0642, -0.0738, -0.0017, -0.0243, -0.0054, 0.0757, -0.0254, 0.0050,
# 0.0519, -0.0695, 0.0318, -0.0042, -0.0189, -0.0263, -0.0627, -0.0691,
# 0.0713, -0.0696, -0.0672, 0.0297, 0.0102, 0.0040, 0.0830, 0.0214,
# 0.0714, 0.0327, -0.0582, -0.0354, 0.0621, 0.0475, 0.0490, 0.0331,
# -0.0111, -0.0469, -0.0695, -0.0062, -0.0432, -0.0132, -0.0856, -0.0219,
# -0.0185, -0.0517, 0.0017, -0.0788, -0.0403, 0.0039, 0.0544, -0.0496,
# 0.0588, -0.0068, 0.0496, 0.0588, -0.0100, 0.0731, 0.0071, -0.0155,
# -0.0872, -0.0504, 0.0499, 0.0628, -0.0057, 0.0530, -0.0518, -0.0049,
# 0.0767, 0.0743, 0.0748, -0.0438, 0.0235, -0.0809, 0.0140, -0.0374,
# 0.0615, -0.0177, 0.0061, -0.0013, -0.0138, -0.0750, -0.0550, 0.0732,
# 0.0050, 0.0778, 0.0415, 0.0487, 0.0522, 0.0867, -0.0255, -0.0264,
# 0.0829, 0.0599, 0.0194, 0.0831, -0.0562, 0.0487, -0.0411, 0.0237,
# 0.0347, -0.0194, -0.0560, -0.0562, -0.0076, 0.0459, -0.0477, 0.0345,
# -0.0575, -0.0005, 0.0174, 0.0855, -0.0257, -0.0279, -0.0348, -0.0114,
# -0.0823, -0.0075, -0.0524, 0.0331, 0.0387, -0.0575, 0.0068, -0.0590,
# -0.0101, -0.0880, -0.0375, 0.0033, -0.0172, -0.0641, -0.0797, 0.0407,
# 0.0741, -0.0041, -0.0608, 0.0672, -0.0464, -0.0716, -0.0191, -0.0645,
# 0.0397, 0.0013, 0.0063, 0.0370, 0.0475, -0.0535, 0.0721, -0.0431,
# 0.0053, -0.0568, -0.0228, -0.0260, -0.0784, -0.0148, 0.0229, -0.0095,
# -0.0040, 0.0025, 0.0781, 0.0140, -0.0561, 0.0384, -0.0011, -0.0366,
# 0.0345, 0.0015, 0.0294, -0.0734, -0.0852, -0.0015, -0.0747, -0.0100,
# 0.0801, -0.0739, 0.0611, 0.0536, 0.0298, -0.0097, 0.0017, -0.0398,
# 0.0076, -0.0759, -0.0293, 0.0344, -0.0463, -0.0270, 0.0447, 0.0814,
# -0.0193, -0.0559, 0.0160, 0.0216, -0.0346, 0.0316, 0.0881, -0.0652,
# -0.0169, 0.0117, -0.0107, -0.0754, -0.0231, -0.0291, 0.0210, 0.0427,
# 0.0418, 0.0040, 0.0762, 0.0645, -0.0368, -0.0229, -0.0569, -0.0881,
# -0.0660, 0.0297, 0.0433, -0.0777, 0.0212, -0.0601, 0.0795, -0.0511,
# -0.0634, 0.0720, 0.0016, 0.0693, -0.0547, -0.0652, -0.0480, 0.0759,
# 0.0194, -0.0328, -0.0211, -0.0025, -0.0055, -0.0157, 0.0817, 0.0030,
# 0.0310, -0.0735, 0.0160, -0.0368, 0.0528, -0.0675, -0.0083, -0.0427,
# -0.0872, 0.0699, 0.0795, -0.0738, -0.0639, 0.0350, 0.0114, 0.0303],
# requires_grad=True) torch.Size([256])
#out.weight Parameter containing:
#tensor([[ 0.0232, -0.0571, 0.0439, ..., -0.0417, -0.0237, 0.0183],
# [ 0.0210, 0.0607, 0.0277, ..., -0.0015, 0.0571, 0.0502],
# [ 0.0297, -0.0393, 0.0616, ..., 0.0131, -0.0163, -0.0239],
# ...,
# [ 0.0416, 0.0309, -0.0441, ..., -0.0493, 0.0284, -0.0230],
# [ 0.0404, -0.0564, 0.0442, ..., -0.0271, -0.0526, -0.0554],
# [-0.0404, -0.0049, -0.0256, ..., -0.0262, -0.0130, 0.0057]],
# requires_grad=True) torch.Size([10, 256])
#out.bias Parameter containing:
#tensor([-0.0536, 0.0007, 0.0227, -0.0072, -0.0168, -0.0125, -0.0207, -0.0558,
# 0.0579, -0.0439], requires_grad=True) torch.Size([10])
四、使用 TensorDataset 和 DataLoader 简化
自己构建数据集,使用 batch 取数据会略显麻烦,因此,我们可以使用 TensorDataset 和 DataLoader 这两个模块进行简化。
from torch.utils.data import TensorDataset
from torch.utils.data import DataLoader
train_ds = TensorDataset(x_train, y_train)
train_dl = DataLoader(train_ds, batch_size=bs, shuffle=True)
valid_ds = TensorDataset(x_valid, y_valid)
valid_dl = DataLoader(valid_ds, batch_size=bs * 2)
def get_data(train_ds, valid_ds, bs):
return (
DataLoader(train_ds, batch_size=bs, shuffle=True),
DataLoader(valid_ds, batch_size=bs * 2),
)- 一般在训练模型时加上 model.train(),这样会正常使用 Batch Normalization 和 Dropout。
- 测试的时候一般选择 model.eval(),这样就不会使用 Batch Normalization 和 Dropout。
import numpy as np
def fit(steps, model, loss_func, opt, train_dl, valid_dl):
for step in range(steps):
model.train()
for xb, yb in train_dl:
loss_batch(model, loss_func, xb, yb, opt)
model.eval()
with torch.no_grad():
losses, nums = zip(
*[loss_batch(model, loss_func, xb, yb) for xb, yb in valid_dl]
)
val_loss = np.sum(np.multiply(losses, nums)) / np.sum(nums)
print('当前step:'+str(step), '验证集损失:'+str(val_loss))
from torch import optim
def get_model():
model = Mnist_NN()
return model, optim.SGD(model.parameters(), lr=0.001)
def loss_batch(model, loss_func, xb, yb, opt=None):
loss = loss_func(model(xb), yb)
if opt is not None:
loss.backward()
opt.step()
opt.zero_grad()
return loss.item(), len(xb)我们也可以像上篇博文一样,使用三行代码进行解决。
train_dl, valid_dl = get_data(train_ds, valid_ds, bs) model, opt = get_model() fit(25, model, loss_func, opt, train_dl, valid_dl) #当前step:0 验证集损失:2.2796445930480957 #当前step:1 验证集损失:2.2440698066711424 #当前step:2 验证集损失:2.1889826164245605 #当前step:3 验证集损失:2.0985311767578123 #当前step:4 验证集损失:1.9517273582458496 #当前step:5 验证集损失:1.7341805934906005 #当前step:6 验证集损失:1.4719875366210937 #当前step:7 验证集损失:1.2273896869659424 #当前step:8 验证集损失:1.0362271406173706 #当前step:9 验证集损失:0.8963696184158325 #当前step:10 验证集损失:0.7927186088562012 #当前step:11 验证集损失:0.7141492074012756 #当前step:12 验证集损失:0.6529350900650024 #当前step:13 验证集损失:0.60417300491333 #当前step:14 验证集损失:0.5643046331882476 #当前step:15 验证集损失:0.5317994566917419 ##当前step:16 验证集损失:0.5047958114624024 #当前step:17 验证集损失:0.4813900615692139 #当前step:18 验证集损失:0.4618900228500366 #当前step:19 验证集损失:0.4443243554592133 #当前step:20 验证集损失:0.4297310716629028 #当前step:21 验证集损失:0.416976597738266 #当前step:22 验证集损失:0.406348459148407 #当前step:23 验证集损失:0.3963301926612854 #当前step:24 验证集损失:0.38733808159828187
到此这篇关于PyTorch中的神经网络 Mnist 分类任务的文章就介绍到这了,更多相关PyTorch神经网络 Mnist 分类任务内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家!
