numpy中的log和ln函数解读
作者:勤奋的大熊猫
这篇文章主要介绍了numpy中的log和ln函数解读,具有很好的参考价值,希望对大家有所帮助。如有错误或未考虑完全的地方,望不吝赐教
numpy的log和ln函数
每次当我想用python实现ln函数时,下意识的就会输入错误的函数代码,这里特来记录一下关于numpy中的ln和log函数正确的调用方式。
ln函数
import numpy as np
class NumpyStudy:
def lnFunction(self):
const = np.e
result = np.log(const)
print("函数ln(e)的值为:")
print(result)
if __name__ == "__main__":
main = NumpyStudy()
main.lnFunction()
"""
函数ln(e)的值为:
1.0
"""我们可以看到得到的值为1,说明在python中,np.log()指代的便是数学中使用的ln函数。
log函数
import numpy as np
class NumpyStudy:
def logFunction(self):
const = 100
result = np.log10(const)
print("函数ln(e)的值为:")
print(result)
if __name__ == "__main__":
main = NumpyStudy()
main.logFunction()
"""
函数ln(e)的值为:
2.0
"""我们可以看到得到的值为2,说明在python中,np.log10()指代的便是数学中使用的lg函数。
前几天看到有一个小伙伴留言说,既然以10和以自然数e为底数的目前都有了,那么以其他数比如2,3,4等等为底数的log函数该怎么办呢?
这里我们需要用到一下数学上的小技巧—换底公式进行一下变换。例如:我们想要求出log以2为底16的值。
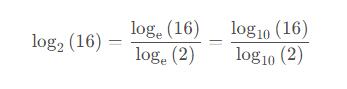
import numpy as np
class NumpyStudy:
def lnFunction(self):
result = np.log(16) / np.log(2)
result1 = np.log10(16) / np.log10(2)
print("函数ln(e)的值为:")
print(result)
print(result1)
if __name__ == "__main__":
main = NumpyStudy()
main.lnFunction()
"""
函数ln(e)的值为:
4.0
4.0
"""可以看到我们最后成功地获取到了正确的结果4.0。用这种方法我们可以获取到以任意数为底数的log函数值。
numpy的部分通用函数
1.数组算术运算符
| 运算符 | 对应的通用函数 | 描述 |
|---|---|---|
| + | np.add | 加法运算(即1+1=2) |
| - | np.substract | 减法运算(即3-2=1) |
| - | np.negative | 负数运算(即-2) |
| * | Nnp.multiply | 乘法运算(即2*3=6) |
| / | np.divide | 除法运算(即3/2=1.5) |
| // | np.floor_divide | 向下整除运算(floor division,即3//2=1) |
| ** | np.power | 指数运算(即2 ** 3=8) |
| % | np.mod | 模/余数(即9%4=1) |
这些都是一元通用函数,写代码时可直接用左栏的运算符代替
x=np.arrange(4) #array([0, 1, 2, 3]) x + 2 #array([2, 3, 4, 5]) np.add(x,2) #array([2, 3, 4, 5])
2.绝对值通用函数np.absolute()
也可以通过np.abs()访问
其对复数的运算是求模
x=np.array([-2, -1, 0, 1, 2]) abs(x) #array([2, 1, 0, 1, 2]) np.absolute(x) #array([2, 1, 0, 1, 2])
3.三角函数
np.sin()np.cos()np.tan()
反三角同理
4.指数和对数
| 表达 | 函数 |
|---|---|
| e^x | np.exp(x) |
| 2^x | np.exp2(x) |
| 3^x | np.power(3, x) |
| ln(x) | np.log(x) |
| log2(x) | np.log2(x) |
| log10(x) | np.log10(x) |
| exp(x)-1 | np.expm1(x) |
| log(1+x) | np.log1p(x) |
以上为个人经验,希望能给大家一个参考,也希望大家多多支持脚本之家。
