pytorch逻辑回归实现步骤详解
作者:Henry_zs
1. 导入库
机器学习的任务分为两大类:分类和回归
分类是对一堆目标进行识别归类,例如猫狗分类、手写数字分类等等
回归是对某样事物接下来行为的预测,例如预测天气等等
这次我们要完成的任务是逻辑回归,虽然名字叫做回归,其实是个二元分类的任务
首先看看我们需要的库文件

torch.nn 是专门为神经网络设计的接口
matplotlib 用来绘制图像,帮助可视化任务
torch 定义张量,数据的传输利用张量来实现
optim 优化器的包,例如SGD等
numpy 数据处理的包
2. 定义数据集
简单说明一下任务,想在一个正方形的区域内生成若干点,然后手工设计label,最后通过神经网络的训练,画出决策边界
假设:正方形的边长是2,左下角的坐标为(0,0),右上角的坐标为(2,2)
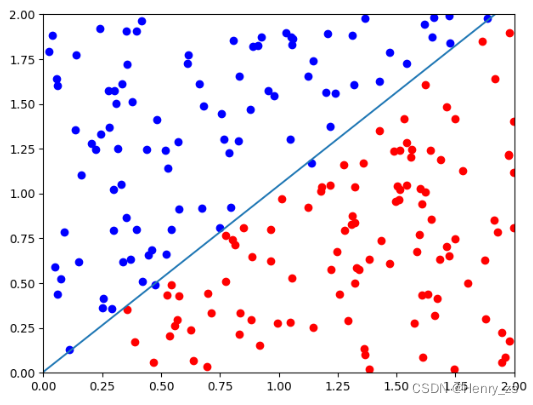
然后我们手工定义分界线 y = x ,在分界线的上方定义为蓝色,下方定义为红色
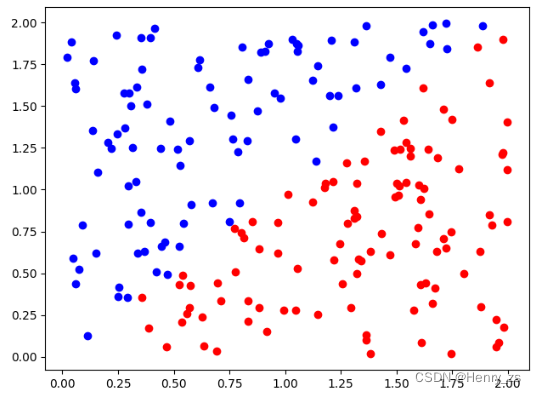
2.1 生成数据
首先生成数据的代码为
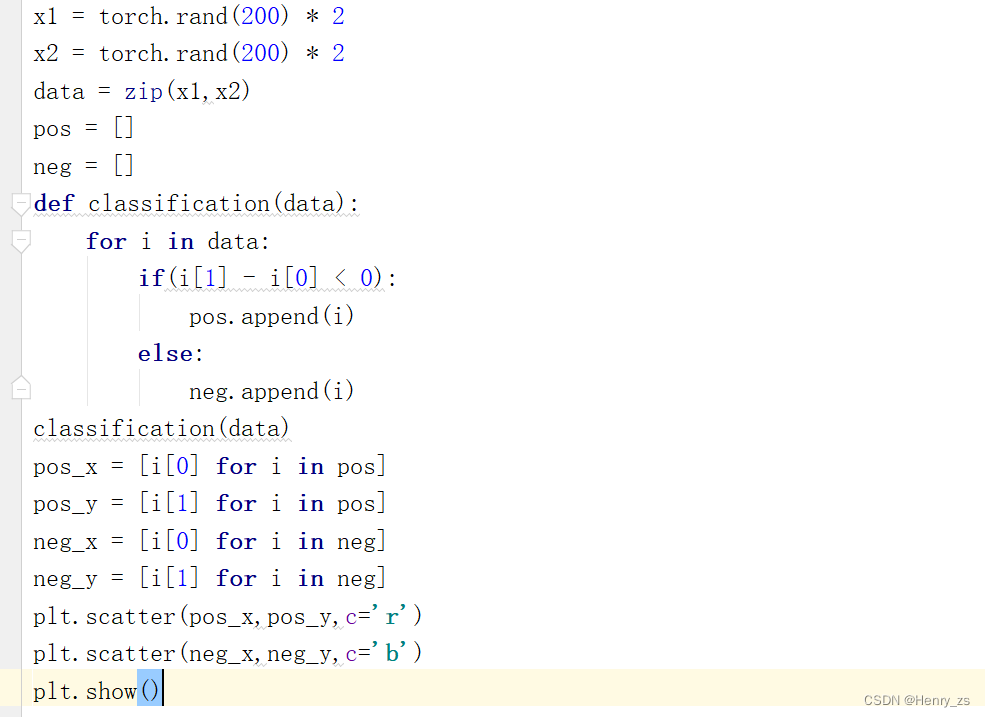
首先通过rand(0-1的均匀分布)生成200个点,并将他们扩大2倍,x1代表横坐标,x2代表纵坐标
然后定义一下分类,这里简单介绍一下zip函数。
zip会将这里的a,b对应打包成一对,这样i对应的就是(1,‘a’),i[0] 对应的就是1 2 3


再回到我们的代码,因为我们要实现的是二元分类,所以我们定义两个不同的类型,用pos,neg存起来。然后我们知道i[1] 代表的是 x2 ,i[0] 代表的是x1 , 所以 x2 - x1 <0 也就是也就是在直线y=x的下面为pos类型。否则,为neg类型

最后,我们需要将pos,neg类型的绘制出来。因为pos里面其实是类似于(1,1)这样的坐标,因为pos.append(i) 里面的 i 其实是(x1,x2) 的坐标形式, 所以我们将pos 里面的第一个元素x1定义为赋值给横坐标,第二个元素x2赋值给纵坐标
然后通过scatter 绘制离散的点就可以,将pos 绘制成 red 颜色,neg 绘制成 blue 颜色,如图
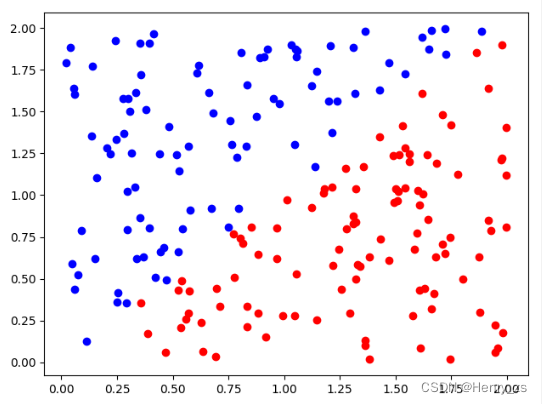
2.2 设置label
我们进行的其实是有监督学习,所以需要label
这里需要注意的是,不同于回归任务,x1不是输入,x2也不是输出。应该x1,x2都是输入的元素,也就是特征feature。所以我们应该将红色的点集设置一个标签,例如 1 ,蓝色的点集设置一个标签,例如 0.
实现代码如下

很容易理解,训练集x_data 应该是所有样本,也就是pos和neg的所以元素。而之前介绍了x1,x2都是输入的特征,那么x_data的shape 应该是 [200,2] 的。而y_data 只有1(pos 红色)类别,或者 0(neg 蓝色)类型,所以y_data 的shape 应该是 [200,1] 的。y_data view的原因是变成矩阵的形式而不是向量的形式
这里的意思是,假如坐标是(1.5,0.5)那么应该落在红色区域,那么这个点的标签就是1
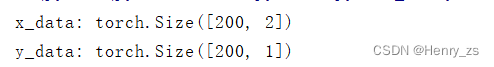
3. 搭建网络+优化器

网络的类型很简单,不再赘述。至于为什么要继承nn.Module或者super那步是干啥的不用管,基本上都是这样写的,记住就行。
需要注意的是我们输入的特征是(n * 2) ,所以Linear 应该是(2,1)
二元分类最后的输出一般选用sigmoid函数
这里的损失函数我们选择BCE,二元交叉熵损失函数。
算法为随机梯度下降

4. 训练

训练的过程也比较简单,就是将模型的预测输出值和真实的label作比较。然后将梯度归零,在反向传播并且更新梯度。
5. 绘制决策边界

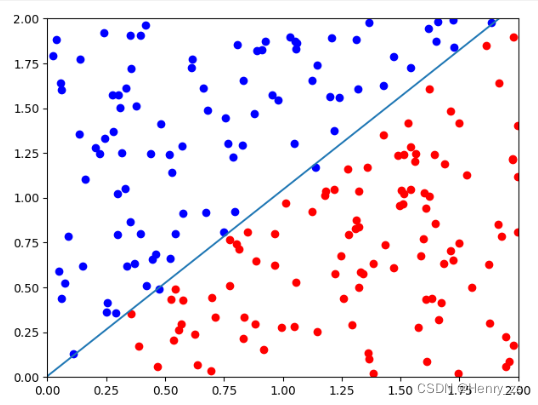
这里模型训练完成后,将w0,w1 ,b取出来,然后绘制出直线
这里要绘制的是w0 * x1+ w1 * x2 + b = 0 ,因为最开始介绍了x1代表横坐标x,x2代表纵坐标y。通过变形可知y = (-w0 * x1 - b ) / w1,结果如图
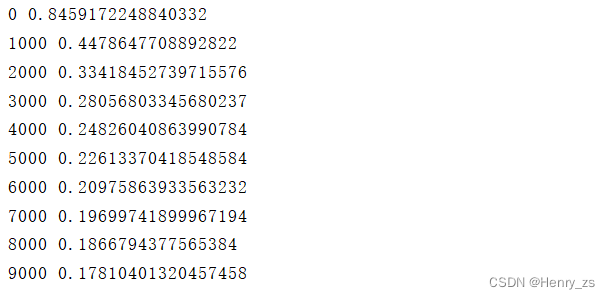
程序输出的损失为
最后,w0 = 4.1911 , w1 = -4.0290 ,b = 0.0209 ,近似等于y = x,和我们刚开始定义的分界线类似
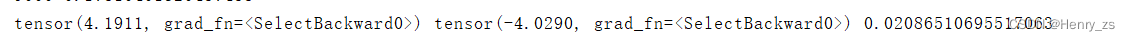
6. 代码
import torch.nn as nn
import matplotlib.pyplot as plt
import torch
from torch import optim
import numpy as np
torch.manual_seed(1) # 保证程序随机生成数一样
x1 = torch.rand(200) * 2
x2 = torch.rand(200) * 2
data = zip(x1,x2)
pos = [] # 定义类型 1
neg = [] # 定义类型 2
def classification(data):
for i in data:
if(i[1] - i[0] < 0):
pos.append(i)
else:
neg.append(i)
classification(data)
pos_x = [i[0] for i in pos]
pos_y = [i[1] for i in pos]
neg_x = [i[0] for i in neg]
neg_y = [i[1] for i in neg]
plt.scatter(pos_x,pos_y,c='r')
plt.scatter(neg_x,neg_y,c='b')
plt.show()
x_data = [[i[0],i[1]] for i in pos]
x_data.extend([[i[0],i[1]] for i in neg])
x_data = torch.Tensor(x_data) # 输入数据 feature
y_data = [1 for i in range(len(pos))]
y_data.extend([0 for i in range(len(neg))])
y_data = torch.Tensor(y_data).view(-1,1) # 对应的标签
class LogisticRegressionModel(nn.Module): # 定义网络
def __init__(self):
super(LogisticRegressionModel,self).__init__()
self.linear = nn.Linear(2,1)
self.sigmoid = nn.Sigmoid()
def forward(self,x):
x = self.linear(x)
x = self.sigmoid(x)
return x
model = LogisticRegressionModel()
criterion = nn.BCELoss()
optimizer = optim.SGD(model.parameters(),lr =0.01)
for epoch in range(10000):
y_pred = model(x_data)
loss = criterion(y_pred,y_data) # 计算损失值
if epoch % 1000 == 0:
print(epoch,loss.item()) # 打印损失值
optimizer.zero_grad() # 梯度清零
loss.backward() # 反向传播
optimizer.step() # 梯度更新
w = model.linear.weight[0] # 取出训练完成的结果
w0 = w[0]
w1 = w[1]
b = model.linear.bias.item()
with torch.no_grad(): # 绘制决策边界,这里不需要计算梯度
x= torch.arange(0,3).view(-1,1)
y = (- w0 * x - b) / w1
plt.plot(x.numpy(),y.numpy())
plt.scatter(pos_x,pos_y,c='r')
plt.scatter(neg_x,neg_y,c='b')
plt.xlim(0,2)
plt.ylim(0,2)
plt.show()程序结果
到此这篇关于pytorch逻辑回归实现步骤详解的文章就介绍到这了,更多相关pytorch逻辑回归内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家!
