关于二分法查找Java的实现及解析
作者:空指针异常1
这篇文章主要介绍了关于二分法查找Java的实现及解析,具有很好的参考价值,希望对大家有所帮助。如有错误或未考虑完全的地方,望不吝赐教
二分法查找
概述
二分查找也称折半查找(Binary Search),它是一种效率较高的查找方法。
但是,折半查找要求线性表必须采用顺序存储结构,而且表中元素按关键字有序排列。
归并排序即运用了二分法的思想。首先需要一个由小到大排序好的数组,先对比中间的值,如果比要找的大,则向前找,取中间值前面的一半再找中间值再对比。
如果比要找的小,则向后找,取中间值后面的一半再取中间值再对比。
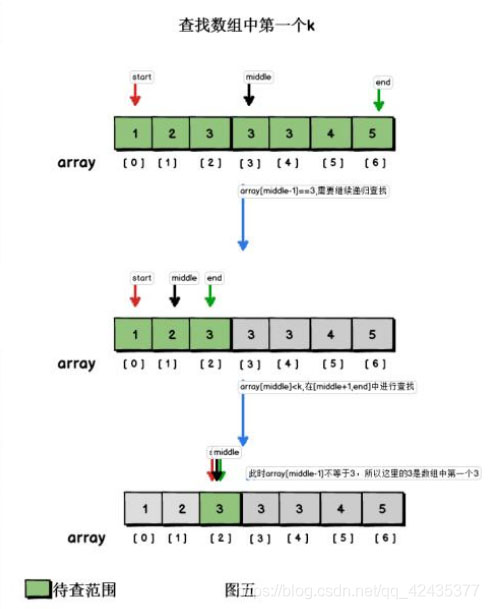
递归实现
这里,我使用了递归的方法进行实现。
首先需要确认查找的范围,即有一个左索引和右索引,每次取(left+right)/2为中间值,比较要查找的元素和中间值的大小,若中间值大,则向前找,即递归范围为left ,mid-1。反之向右找,即递归范围mid+1,right。若相等即为找到。
但是需要继续向此索引的前后找找看有没有和其相等的值,一并加入到集合中,最后返回这个集合。
递归实现代码
package search;
import java.util.ArrayList;
import java.util.List;
public class BinarySearch {
public static void main(String[] args) {
int[] array = {1,1,1,2,3,4,5,6,7};
List<Integer> integers = binarySearch(array, 0, array.length - 1, 1);
// for (Integer integer : integers) {
// System.out.print(integer+ " ");
// }
System.out.println(integers);
}
public static List<Integer> binarySearch(int[] array, int left, int right, int value){
//如果左索引大于右索引,则说明全部遍历完了,也没有找到相应的值,返回空集合即可
if (left>right){
return new ArrayList<Integer>();
}
//获取中间值的下标(二分)
int mid = (left+right)/2;
//如果要找的值比中间值小,则继续向左找
if (value < array[mid]){
return binarySearch(array, left, mid-1, value);
//要找的值比中间值小大,则向右找
}else if (value > array[mid]){
return binarySearch(array, mid+1, right, value);
//否则,说明相等,找到了
}else {
//找到一个,还需要向左右找找看有没有相同的值
List<Integer> resultList = new ArrayList();
//向左循环找,如果有,则加入到集合中
int temp = mid - 1;
while (temp>=0 && array[temp] == value){
resultList.add(temp);
temp -= 1;
}
//向右循环找,如果有,则加入到集合中
temp = mid + 1;
while (temp < array.length && array[temp] == value){
resultList.add(temp);
temp += 1;
}
//将一开始找到的那个索引页加入到集合中。
resultList.add(mid);
return resultList;
}
}
//以下这段代码来自百度百科,供大家参考。
public static int binarySearch(Integer[] srcArray, int des) {
//定义初始最小、最大索引
int start = 0;
int end = srcArray.length - 1;
//确保不会出现重复查找,越界
while (start <= end) {
//计算出中间索引值
int middle = (end + start)>>>1 ;//防止溢出
if (des == srcArray[middle]) {
return middle;
//判断下限
} else if (des < srcArray[middle]) {
end = middle - 1;
//判断上限
} else {
start = middle + 1;
}
}
//若没有,则返回-1
return -1;
}
}
循环实现代码(非递归)
package search;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
/**
* @Author: sshdg
* @Date: 2020/9/21 9:22
*/
public class BinarySearch2 {
public static void main(String[] args) {
int[] array = {1,1,1,1,1,2,3,4,5,6,7};
System.out.println(BinarySearch2.binarySearch(array, 7));
}
public static List<Integer> binarySearch(int[] array, int key){
List<Integer> resultList = new ArrayList<>();
int start = 0;
int end = array.length - 1;
while (start <= end){
int mid = (start + end) / 2;
int midValue = array[mid];
if (key > midValue){
//key比中间值大。向右找
start = mid + 1;
} else if (key < midValue){
//key比中间值小。向左找
end = mid - 1;
} else {
//否则就找到了
//先向左找有没有相同值
int temp = mid -1;
while (temp >= start && array[temp] == key){
resultList.add(temp);
temp -= 1;
}
//将一开始找到的加入结果集
resultList.add(mid);
//再向右找找有没有相同值
temp = mid + 1;
while (temp <= end && array[temp] == key){
resultList.add(temp);
temp += 1;
}
break;
}
}
return resultList;
}
}
二分法查找(递归、循环)
public class BinarySearch {
/**
* @author JadeXu
* @// TODO: 2020/12/7 二分查找
* 思路:
* 1、获取数组的中间值,先获取下标,方便多次查找
* 奇数位的数组直接获取中间位,偶数位的数组获取中间的第一位或第二位都可,一般获取第一位(因为与奇数位获取中间值的方法一样)
* 2、获取查找的区间范围,start:区间开始的下标,end:区间结束的下标
* 3、判断查找的数和中间位的数是否相同
* 相同时,直接返回需要的数据,跳出方法
* 大于时,即数可能在中间值右边的区间内,此时start = mid+1,即mid往后移一位,就得到了中间值右边区间的开始下标
* 小于时,即数可能在中间值左边的区间内,此时end = mid-1,即mid往前移一位,就得到了中间值左边区间的结束下标
* 当一个区间里,开始下标小于等于结束下标时,该区间才是有效区间,才能继续查找。否则无效,返回找不到,跳出方法
*/
//循环
/**
* @param arr 已经升序好的int[]
* @param num 需要查找的数字
* @return 找到则返回下标,没找到则返回-1
*/
private static int binarySearchByCycle(int[] arr,int num) {
int start = 0;
int end = arr.length - 1;
while (start <= end){
int mid = (start + end) / 2;
if(num == arr[mid]){
return mid;
}else if(num > arr[mid]){
start = mid + 1;
}else {
end = mid - 1;
}
}
return -1;
}
//递归
/**
* @param arr 已经升序好的int[]
* @param num 需要查找的数字
* @param start 区间开始下标
* @param end 区间结束下标
* @return 找到则返回下标,没找到则返回-1
*/
private static int binarySearchByRecursion(int[] arr,int num,int start,int end) {
int mid = (start + end) / 2;
if(num == arr[mid]){
return mid;
}else if(num > arr[mid]){
start = mid + 1;
}else {
end = mid - 1;
}
if(start <= end){
mid = binarySearchByRecursion(arr,num,start,end); //递归继续寻找
}else {
mid = -1;
}
return mid;
}
}
以上为个人经验,希望能给大家一个参考,也希望大家多多支持脚本之家。
