C语言详细图解浮点型数据的存储实现

在引入知识之前，先来看一个案例，就知道了解浮点型数据存储的重要性与必要性。

举个例子：

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
int main()
{
	int num = 9;
	float *pnum = (float *)&num;//强制转换类型
	printf("n的值为:%d\n",n);
	printf("*pFloat的值为:%f\n",*pnum);
	*pnum = 9.0;
	printf("num的值为:%d\n",n);
	printf("*pFloat的值为:%f\n",*pnum);
	return 0;
}

一般情况下我们都会认为*pnum打印的就是n的值，只不过是以浮点型打印出来，所以是9.000000啊，然后下面的n又因为*pnum的修改，加之因为%d输出，所以还是9啊，但是结果不是，打印出来的结果如下图所示：

结果与我们想的有很大的偏差。。。。。那就有必要让我们来了解浮点型数据的存储啦！

1.首先，根据上面的实例，我们可以发现整型和浮点型数据的存储方法是不一样的！

2.那么浮点型数据是怎么存储的呢？

（1）根据国际标准IEEE(电子和电子工程协会)754，任意一个二进制浮点数V可以表示为下面的形式：

## (-1)^S * M * 2^E

## (-1)^S 表示符号位，当S=0时，V为正数；当S=1时，V为负数。

## M 表示有效数字，且1<=M<2

## 2^E表示指数位

举例来说：十进制的 5.0，写成二进制是 101.0，相当于 1.01 *2^2 。那么，按照上面的V的格式，可以得出S=0，M=1.01，E=2。

十进制的 -5.0，写成二进制是 -101.0 ，相当于 -1.01 * 2^2 。那么，S=1，M=1.01，E=2。

IEEE 754规定对于任意一个浮点数V都可以表示成V=(-1)^s * M *2^E,那我们是不是只要知道S、M、E三个值就可以确定一个浮点数？事实上，c语言内存存储浮点数时，也确实是只存储S、和指数E有关的一个值、和M有关的一个值(注意，这里不是直接存E、M) 详情如下:

相对应的float型是32位的，它的存储空间如下：

相对应的double型是64位的，它的存储空间如下：

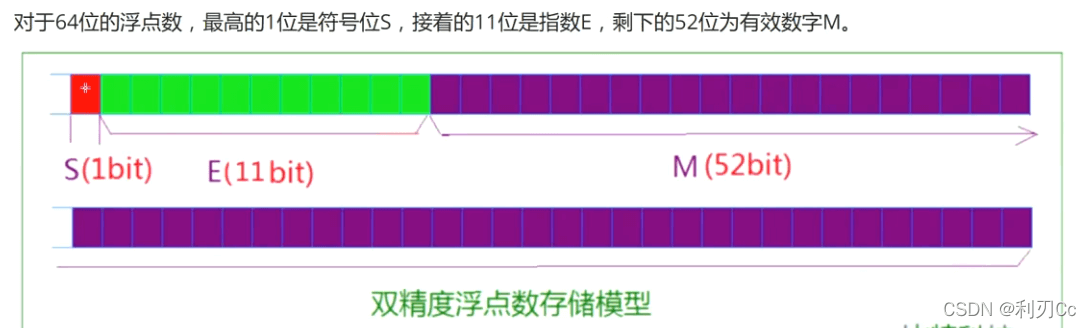
对于M与E的特别规定：

E的使用：

所以我们再对刚才的代码加以解释：

1.首先我们先把n的补码写出来，因为n是正数，所以它的原反补相同。

2.按照上面的方法，把n的补码分解后发现它的E为全0，所以相当于一个无穷小的数字，所以此时*p为0.000000……

3.将*p改成9.0后按照上面的方法，先改成二进制 1001.1，然后写成 (-1)^0 * 1.001 * 2^3，最后按照格式变成补码，存到内存中去，此时补码为01000001000100000000000000000000，而n为整型数据，所以先取出这个补码，又因为其为正数，所以直接将补码转为十进制%d输出：

结果与我们之前执行的结果一致！

浮点型数据存储是很重要的知识点，它也加强了我们对数据存储的了解！

到此这篇关于C语言详细图解浮点型数据的存储实现的文章就介绍到这了,更多相关C语言数据存储内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家！