一文了解mysql索引的数据结构为什么要用B+树

前提： 以下的一些数据结构大家需提前知道，否则看起来会比较有困难，大家也可以按照本文所提到的知识点去主动查阅学习。

1. Hash表？No

因考虑到在数据检索的过程中经常会有范围的查询（如下），而hash表不能提供这种功能。

SELECT * FROM hero WHERE age>5 AND age<20;

使用哈希算法实现的索引虽然可以做到快速检索数据，但是没办法做数据高效范围查找，因此哈希索引是不适合作为 Mysql 的底层索引的数据结构。

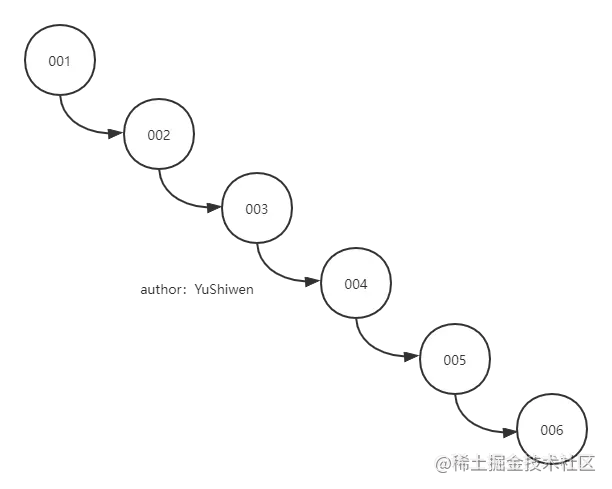
2. 二叉查找树(BST)？No

二叉查找树（Binary Search Tree）虽然可以达到范围搜索，但是在树的插入过程中，如果插入的数据本来就是有顺序的，那么就会形成一条链（如下），它的最坏情况是O(n)。 

3. 红黑树？No

红黑树虽然看似达到了平衡状态，但是也会有极端情况存在，和上述BST树一样，虽然不会成为链状，但是红黑树会存在右倾的现象。 

在数据库中的基本主键自增操作，主键一般都是数百万数千万的，如果红黑树存在这种问题，对于查找性能而言也是巨大的消耗，我们数据库不可能忍受这种无意义的等待的。

4. 平衡二叉树(AVL)？差那么二点意思

平衡二叉树，英文翻译为Balanced Binary Tree，为啥叫AVL呢？ AVL 是大学教授G.M. Adelson-Velsky 和 E.M. Landis 名称的缩写，他们提出的平衡二叉树的概念，为了纪念他们，将平衡二叉树称为 AVL树。

AVL树本质上是一颗二叉查找树，但是它又具有以下特点：

• 它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，
• 左右两个子树也都是一棵平衡二叉树。

它不存在红黑树这种右倾的现象，也具备数据高效范围查找的能力，但是数据库查询数据的瓶颈在于磁盘的IO，树节点在磁盘空间中存储可能是不连续的，假设我们一次IO读取一个树的节点，此次读入内存的这页中没有其他树的节点，那么每读取一个树的节点，就要进行一次IO，这是多么消耗时间啊，所以我们设计数据库索引时需要首先考虑怎么尽可能减少磁盘 IO 的次数。 磁盘读取依靠的是机械运动，分为寻道时间、旋转延迟、传输时间三个部分，这三个部分耗时相加就是一次磁盘IO的时间；这个花费的时间成本是内存访问的十几万倍左右。 正是由于磁盘IO是非常昂贵的操作，所以计算机操作系统对此做了优化：预读；每一次IO时，不仅仅把当前磁盘地址的数据加载到内存，同时也把相邻数据也加载到内存缓冲区中。因为局部预读原理说明：当访问一个地址数据的时候，与其相邻的数据很快也会被访问到。每次磁盘IO读取的数据我们称之为一页（page）。一页的大小与操作系统有关，一般为4k或者8k。这也就意味着读取一页内数据的时候，实际上发生了一次磁盘IO。

相关术语解释：

扇区(sector)：

• 磁盘上的每个磁道被等分成多个弧段，这个弧段便称作扇区（sector）。
• 扇区是磁盘物理层面的名称，它是实际发生读写的最底层。

磁盘块(IO Block)：

• 操作系统不与扇区直接进行交互，因为一般情况下一个扇区是512byte，如果1T去用512byte进行划分，那划分的地址空间太多了，为了让操作系统能够寻址到更大的地址空间，操作系统将相邻的扇区组合在一起，形成一个块，对块进行管理。每个磁盘块可以包括 2、4、8、16、32 或 64 个扇区，这便是磁盘块（IO Block）。
• 磁盘块是操作系统中出现的名称，文件系统读写数据的最小单位，它同时也被叫做磁盘簇。

页(page)：

• 页是内存中出现的名称，它是内存的最小存储单位，页的大小通常为磁盘块大小的 2^n 倍。

5. B-tree(B-树也称B树)？差那么一点意思

B树是一种平衡的多叉树，B树相比于平衡二叉树(AVL)，它能够在单个节点中存储大量键，也降低了树的高度，从而减少了IO的次数。 

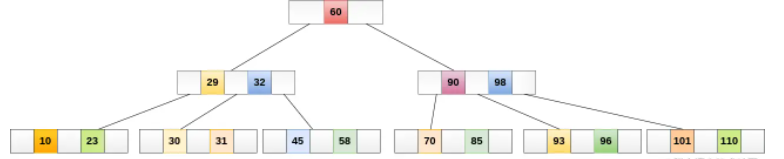
B树的节点中存储的是数据，单个节点存储的内容还是太少了，如何让一个节点存储的内容更多呢？B+树它来了。

6. B+树

在节点中存储某段数据的首地址，并且B+树的叶子节点用了一个链表串联起来，便于范围查找。 

B+树高度降低，减少了磁盘 IO。其次，B+树的叶子节点是真正数据存储的地方，叶子节点用了链表连接起来，这个链表本身就是有序的，在数据范围查找时，更具备效率。因此 Mysql 的索引用的就是 B+树，B+树在查找效率、范围查找中都有着非常不错的性能。

到此这篇关于一文了解mysql索引的数据结构为什么用B+树的文章就介绍到这了,更多相关mysql B+树内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家！