java版十大排序经典算法:完整代码(3)
作者:牛哄哄的柯南
优秀的文章也不少,但是Java完整版的好像不多,我把所有的写一遍巩固下,同时也真诚的希望阅读到这篇文章的小伙伴们可以自己去从头敲一遍,不要粘贴复制!希望我的文章对你有所帮助,每天进步一点点
归并排序
简单解释:该算法是采用分治法,把数组不断分割,直至成为单个元素,然后比较再合并(合并的过程就是两部分分别从头开始比较,取出最小或最大元素的放到新的区域内,继续取两部分中最大或最小的元素,直到这两部分合并完,最后所有的都合并完,最后形成完整的有序序列)
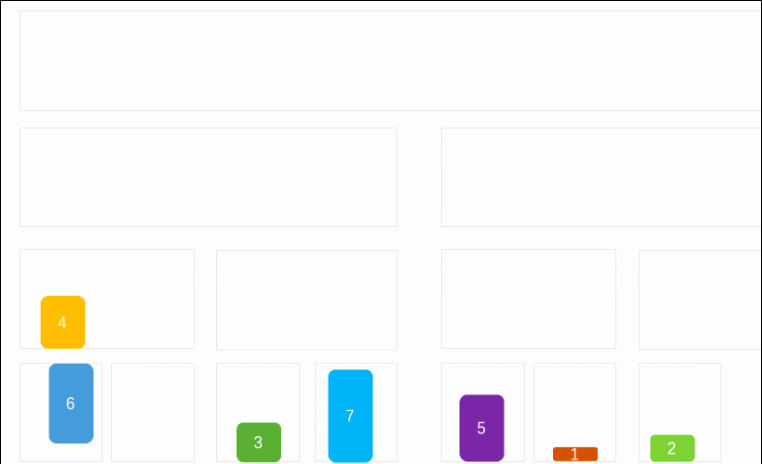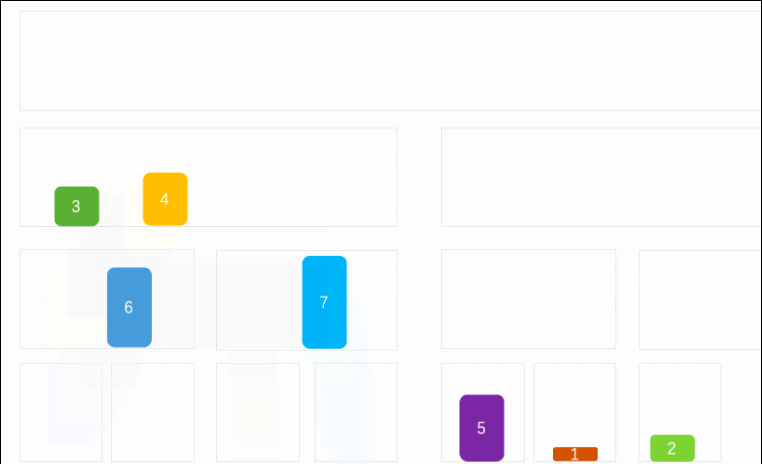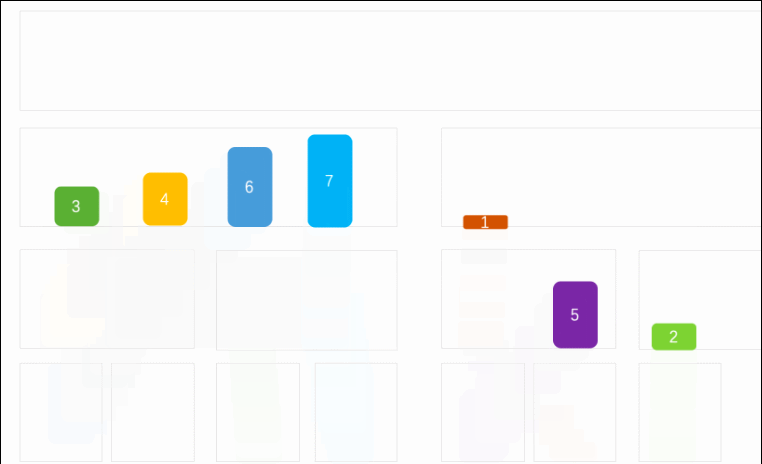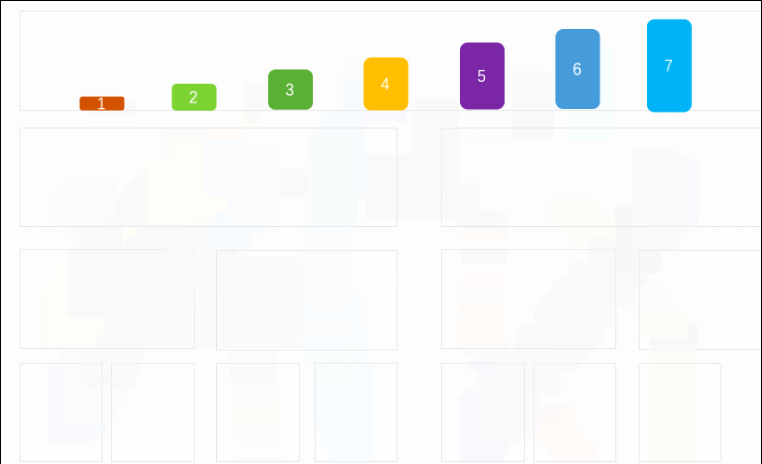
完整代码:
package com.keafmd.Sequence;
/**
* Keafmd
*
* @ClassName: MergeSort
* @Description: 归并排序
* @author: 牛哄哄的柯南
* @date: 2021-06-24 10:35
*/
public class MergeSort {
//归并排序
public static void mergeSort(int []arr ,boolean ascending){
int[] temp = new int[arr.length]; //在排序前,先建好一个长度等于原数组长度的临时数组,避免递归中频繁开辟空间
mergeSort(arr,0,arr.length-1,temp,ascending);
}
public static void mergeSort(int []arr){
mergeSort(arr,true);
}
/**
*
* @param arr 传入的数组
* @param left 当前子数组的起始下标
* @param right 当前子数组的结束下标
* @param temp 拷贝暂存数组
*/
public static void mergeSort(int []arr,int left,int right,int[] temp,boolean ascending){
if(left<right){ //这里是递归结束的条件,我们是对半分,那当left==right的时候肯定大家都是只有一个元素了。
//对半分,比如总长度是10,left=0,right=9,mid=4确实是中间分了,0~4,5~9
//当长度9,left=0,right=8,mid=4,0~4,5~8
int mid = left + (right-left)/2; // 防止越界的写法
//int mid = (left+right)/2;
mergeSort(arr,left,mid,temp,ascending); //左边归并排序,使得左子序列有序
mergeSort(arr,mid+1,right,temp,ascending); //右边归并排序,使得右子序列有序
merge(arr,left,mid,right,temp,ascending); //将两个有序子数组合并操作
}
}
private static void merge(int[] arr,int left,int mid,int right,int[] temp,boolean ascending){
int i = left; //左序列起始下标
int j = mid+1; //右序列起始下标
int t = 0; //临时数组指针
while(i<=mid&&j<=right){
if(ascending?arr[i]<arr[j]:arr[i]>arr[j]){ //比较两个序列第一个元素谁小,谁小先拷贝谁到temp,然后对应子序列下标加1
temp[t++] = arr[i++];
}else {
temp[t++] = arr[j++];
}
}
while(i<=mid){ //将左边剩余元素填充进temp中——左序列有一些数总是比右边的大的数
temp[t++] = arr[i++];
}
while(j<=right){ //将右序列剩余元素填充进temp中——右序列有一些数总是比左边的大的数
temp[t++] = arr[j++];
}
t = 0;
//将temp中的元素全部拷贝到原数组中
while(left<=right){
arr[left++] = temp[t++];
}
}
}
插入排序
简单解释:最简单的理解就是打地主时我们拿到牌后的整理过程,从第二个牌(假设我们拿起来这个牌开始比较)开始,(说下升序)从后往前比较如果比前面的那个牌小,就把牌往后移动,直到找到一个合适的位置(这个位置的前面的那个牌不比这个要放下的牌大)就把这个牌放到这个位置,慢慢的前面的部分变得有序,直至全部有序即可。
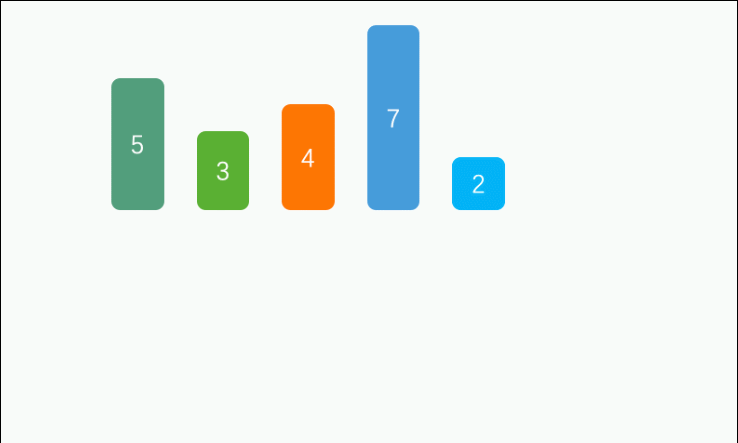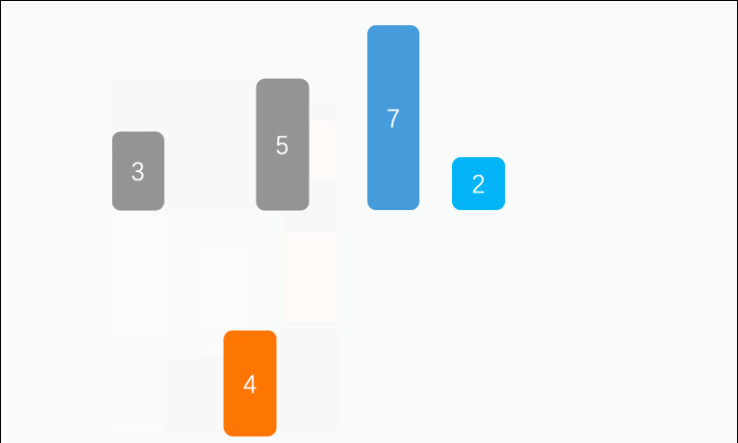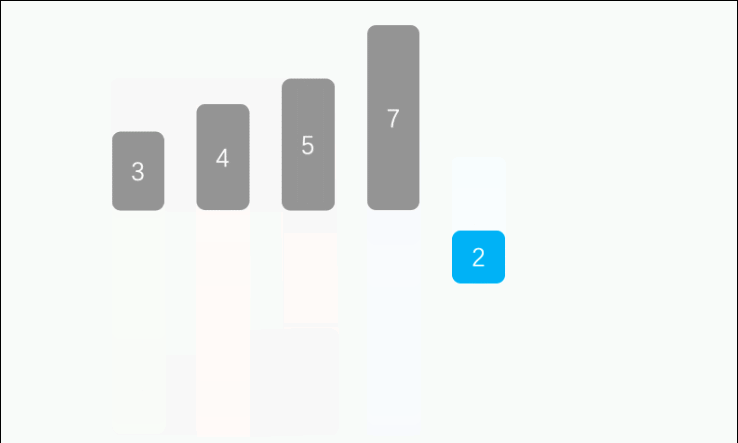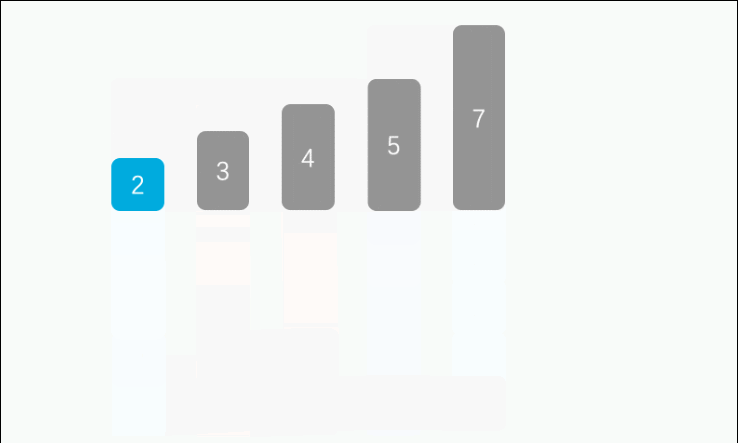
完整代码:
package com.keafmd.Sequence;
/**
* Keafmd
*
* @ClassName: StraghtInsertSort
* @Description: 插入排序
* @author: 牛哄哄的柯南
* @date: 2021-06-24 10:36
*/
public class StraghtInsertSort {
//插入排序
public static void straghtInsertSort(int[] arr) {
straghtInsertSort(arr, true);//默认进行升序
}
public static void straghtInsertSort(int[] arr, boolean ascending) {
for (int i = 1; i < arr.length; i++) {
int temp = arr[i];
int j=0; //这就是那个合适的位置
for (j = i - 1; j >= 0 && (ascending ? temp < arr[j] : temp > arr[j]); j--) {
arr[j + 1] = arr[j];
}
//把牌放下,为啥是j+1,
//是因为上面的循环遍历到不符合情况的时候 j是合适的位置的前面的那个数的位置
//有点拗口,但是就是这个意思,看图方便理解下
arr[j + 1] = temp;
}
}
}
希尔排序
简单解释:希尔排序是插入排序的改进版,我们理解一个叫做下标差的的东西,也就是下面那个图中的增量d,初始下标差为arr.length/2,然后继续/2,对在同一下标差(相当于把这几个数单独拿出来了)的若干个数进行插入排序即可。


完整代码:
package com.keafmd.Sequence;
/**
* Keafmd
*
* @ClassName: ShellSort
* @Description: 希尔排序
* @author: 牛哄哄的柯南
* @date: 2021-06-24 10:39
*/
public class ShellSort {
public static void shellSort(int[] arr) {
shellSort(arr,true);
}
public static void shellSort(int[] arr,boolean ascending) {
for(int d = arr.length/2;d>0;d/=2){
for(int i=d;i< arr.length;i++){
int temp = arr[i];
int j=0;
for(j=i-d;j>=0&&(ascending?temp<arr[j]:temp>arr[j]);j-=d){
arr[j+d]=arr[j];
}
arr[j+d] = temp;
}
}
}
}
总结
本篇文章就到这里了,希望能给你带来帮助,也希望您能够多多关注脚本之家的更多内容!
