python实现线性回归的示例代码

2009-11-26 17:00:05 作者：邀_灼灼其华

本文主要介绍了python实现线性回归的示例代码，文中通过示例代码介绍的非常详细，对大家的学习或者工作具有一定的参考学习价值，需要的朋友们下面随着小编来一起学习学习吧

1、导入第三方库

import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
import numpy as np

2、生成数据集

def generateData():
    X = []
    y = []
    for i in range(0, 100):
        tem_x = []
        tem_x.append(i)
        X.append(tem_x)
        tem_y = []
        tem_y.append(i + 2.128 + np.random.uniform(-15,15))
        y.append(tem_y)
        plt.scatter(X, y, alpha=0.6)
    return X,y

3、计算残差平方

def residual_sum_of_squares(y_true, y_pred):
    # 计算残差
    residuals = y_true - y_pred    
    # 计算残差平方
    squared_residuals = residuals ** 2   
    # 计算残差平方和
    rss = np.sum(squared_residuals)    
    return rss

4、训练模型

if __name__ == '__main__':
    np.random.seed(0)
    X,y = generateData()
    print(len(X))
    X_train,X_test, y_train, y_test = train_test_split(X, y, test_size=0.2,
    random_state=0)
    regressor = LinearRegression()
    regressor.fit(X_train, y_train)
    y_result = regressor.predict(X_test)
    plt.plot(X_test, y_result, color='red',alpha=0.6, linewidth=3,
    label='Predicted Line')
    plt.show()
    
    # 提取模型的斜率和截距
    slope = regressor.coef_[0]
    intercept = regressor.intercept_

    # 输出拟合函数
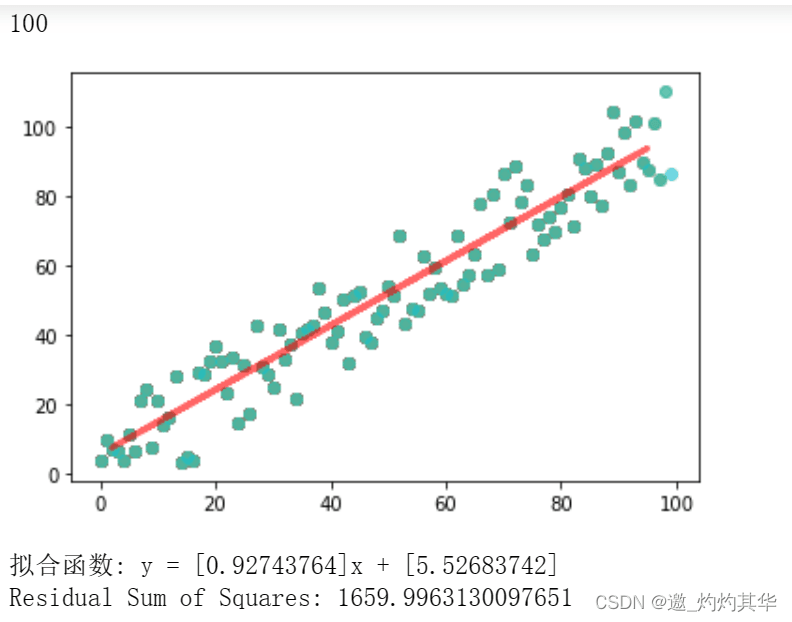
    print(f"拟合函数: y = {slope}x + {intercept}")
    
    # 计算残差平方和
    rss = residual_sum_of_squares(y_test, y_result)
    print("Residual Sum of Squares:", rss)

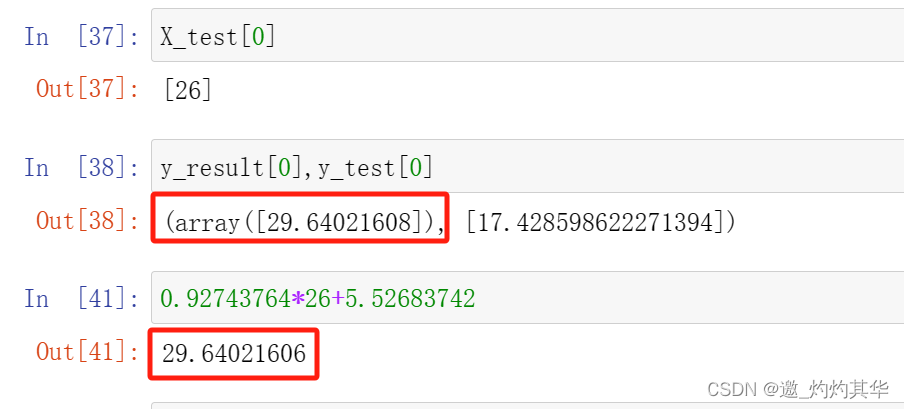
在这里插入图片描述

5、数据验证

在这里插入图片描述

6、模型优缺点

优点
运算速度快。由于算法很简单，而且符合非常简洁的数学原理，不管是建模速度，还是预测速度都
是非常快的。
可解释性强。由于最终我们可以得到一个函数公式，根据计算出的公式系数就可以很明确地知道每
个变量的影响大小。
对线性关系拟合效果好。当然，相比之下，如果数据是非线性关系，那么就不合适了。

缺点
预测的精确度较低。由于获得的模型只是要求最小的损失，而不是对数据良好的拟合，所以精确度略低。
不相关的特征会影响结果。对噪声数据也比较难处理，所以在数据处理阶段需要剔除不相关的特征以及噪声数据。
容易出现过拟合。尤其在数据量较少的情况下，可能出现这种问题。

到此这篇关于python实现线性回归的示例代码的文章就介绍到这了,更多相关python 线性回归内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家！